Малохвильовий перетворювач WAVELET, страница 3

а) бажана передаточна функція  з граничного (рис.а) є передаточною функцією інтегрального ФНЧ:

б) оскільки передаточна функція цифрового фільтра є дискретною трансформацією, вона завжди є періодичною (рис. б);

в) передаточна функція реалізованого фільтра буде . Спочатку визначається як ряд Фурє, і він буде тим краще апроксимувати бажану періодичну функцію , чим більше членів буде включати в себе. Оскільки число коефіцієнтів фільтра мусить бути скінченним, ряд Фур’є повинен бути десь обірваним і з’явиться різниця між  та ;

г) метод найменших квадратів Гауса служить як критерій апроксимації. Інтеграл по квадратних різницях повинен мати мінімальне значення:

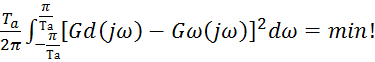
д) похибка апроксимації мінімальна в середньому квадратичному, якщо вагові коефіцієнти шуканого фільтра є коефіцієнтами ряду Фур’є розвитку в ряд .

За допомогою наведеного вище алгоритму можна визначити шукані коефіцієнти фільтра. Бажаним є ідеальний ФНЧ з передаточною функцією:

 при

 – парна функція

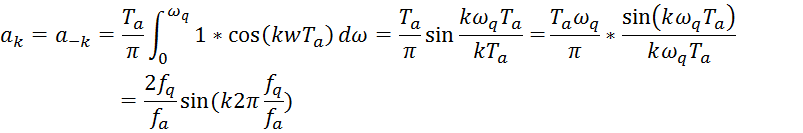
Коефіцієнти  обчислюються із функції розщеплення, в якій аргументом буде відношення граничної частоти до частоти вибірок. Ці обидві величини в усіх випадках зв’язані одна з одною. Якщо в уже визначеному фільтрі буде змінена частота дискретизації, то зміниться також і гранична частота. За цієї причини при визначенні параметрів фільтрів буде часто обчислюватися гранична кругова частота, віднесена до частоти дискретизації.

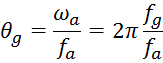
Коефіцієнти ФНЧ тепер будуть мати вигляд:

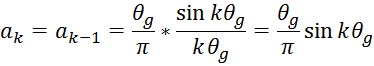
Коефіцієнти ФВЧ шукаються виходячи з уже відомих коефіцієнтів ФНЧ: а_{к фвч}=а_квч - а_{к фнч} а_квч – коефіцієнти високочастотного фільтра.

3.Дискретне Waveletsперетворення

Дискретне Wavelet перетворення в своїй основі має ієрархічну структуру. Wavelet перетворення спочатку застосовується до повного вектора довжиною N, потім до «згладженого» вектора N₁₂, а потім до «згладженого-згладженого» вектора довжиною N₁₄ і т.д. аж поки не залишиться незначне число компонентів. Таку процедуру називають «пірамідальним алгоритмом».

Вихід DWT складається із залишкових компонентів і всіх «детальних компонентів», що були накопичені під час всього перетворення. На рис. показана структура DWT перетворення, яка використовується в даному курсовому проекті і розрахована на 16 вхідних вибірок і відповідно на 3 послідовно включені комірки (які зображені на малюнку).

Значення  і-го рівня (і-та комірка) є назване «Wavelet коефіцієнтом» початкового вектора даних, кінцеві значення В₃₁, В₃₂ повинні називатись «базові функціональні коефіцієнти», хоча насправді термін «Wavelet коефіцієнтів» використовується для С₃₁, С₃₂ і кінцевих В₃₁, В₃₂. В курсовому проекті С₃₁, С₃₂, В₃₁, В₃₂ називаються коефіцієнтами Wavelets.

Для організації IDWT необхідно просто обернути процедуру, починаючи з найменшого рівня ієрархії. При цьому схема зворотнього DWT перетворення формує сигнали запиту на передачу коефіцієнтів С₁, С₂, С₃. Ці запити поступають на схему прямого DWT перетворення, яка визначає необхідний коефіцієнт.

В схемі прямого DWT перетворення поступово. Переходячи від комірки 1 до комірки 3, розраховуються вектори коефіцієнтів С₁, С₂, С₃. Число вибірок зменшується в 2 рази з кожним кроком. В результаті 8-ми розрядні вибірки коефіцієнтів записуємо в пам'ять.

Схема IDWT формує запити на передачу коефіцієнтів С₁, С₂, С₃. Вибірки кожного вектора передаються послідовно так як і записувались в пам'ять. При поступлені кожної вибірки у вихідний порт формується сигнал «Дані готові», який передається на схему IDWT.

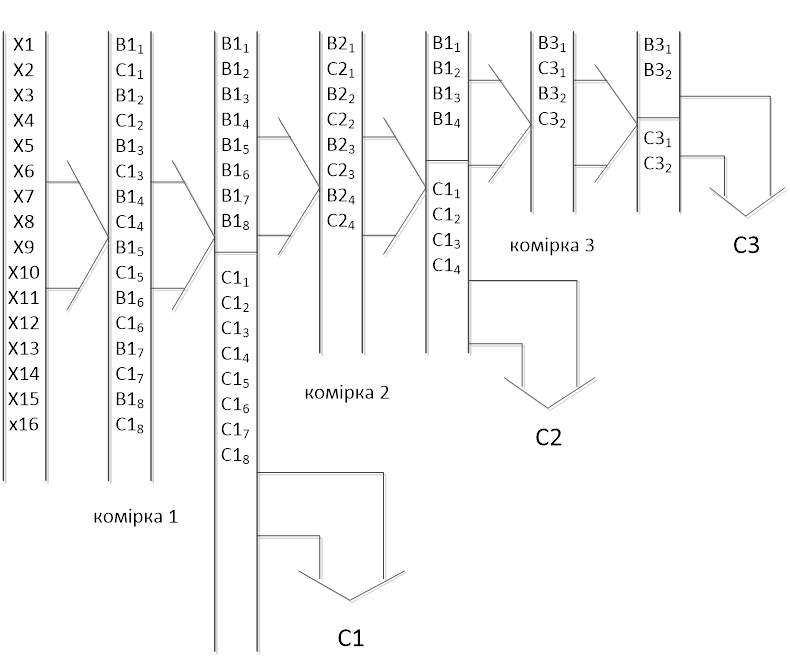
Рис.3. Структура DWT перетворення

Послідовність передачі і запитів і коефіцієнтів виглядає наступним чином:

1.  Формується запит на передачу С₃.

2.  Передаються вектори В₃, С₃ послідовно.

3.  Відбувається IDWT перетворення, в результаті якого отримаємо В₂.

4.  Формується запит на передачу С₂.

5.  Послідовно передаються вибірки вектора С₂.