Информатика и выч. техника \ Информатика

Малохвильовий перетворювач WAVELET, страница 2

                                       (7)

Дана дискретизація зроблена до застосування алгоритму і вибір x(t) не залежить від Wavelet чи інших параметрів алгоритму. Згідно з алгоритму Шенса тепер можна знайти коефіцієнти Wavelet:

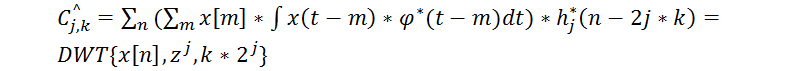(8)

В алгоритмі Шенса передбачена Wavelet апроксимація, яка важлива, оскільки її точність визначає точність всього алгоритму. Вона включає в себе два кроки. Перший – визначити високо пропускний фільтр g[n], другий – визначити високо пропускний фільтр h[n].

У випадку смугового-обмеженого Wavelet  розв’язок «двомасштабного різницевого рівняння»

                                                  (9)

буде наступним:

             ;

Іншим рішенням є рівняння (5) є класична інтерполяційна функція «базовий сплайн» деякого степеня к, перетворення Фур’є якого:

                                                                    (10)

Розв’язавши рівняння (5) в частотній області отримаємо:

 n=0…k+1

Одержуємо біноміальний фільтр. Потрібна додаткова умова:

g[n-2]=0, коли

За допомогою DWT  можна обчислити перетворення Wavelet рядів (WST).

При цьому спочатку аналоговий сигнал x(t) дискретизують згідно виразу (6). Тоді дискретний в часі сигнал x[n] обробляють DWT алгоритмом. Коли відбувається процес синтезу, сигнал відновлюють за допомогою IDWT, а далі відбувається інтерполяція (або ЦАП) за формулою:

IDWT{Cj,k}=y[n]

IDWT{Cj,k}=

Для точкового відтворення оригінального сигналу x(t) необхідне точне відтворення пари цифрових наборів.

DWT IDWT
 


      x(t)            A/D                                                                 y[n]      D/A          y(t)

                                                     

Рис. 1. Завершена схема

IDWT алгоритм легко отримати з алгоритму DWT. Структура зворотного перетворення така, що коефіцієнти фільтра g[n], h[n] заміняються на  і   відповідно. Так чи інакше будь-який DWT алгоритм, один раз транспонований, може бути використаний для реалізації IDWT алгоритму. DWT і IDWT вимагають однакової кількості операцій (множень і додавань) на кожне значення.

Структурне обчислення в DWT має вигляд восьми смугових (октавосмугових) наборів фільтрів, які зображені на рис.2. DWT відповідає аналізуючому (розкладаючому) набору.

IDWT відповідає синтезуючому (відтворюючому) набору. g[n], h[n],  ,   – це саме такі фільтри, які представлені у фільтрових наборах. Щоразу, коли використовуємо DWT ми припускаємо, що фільтровий набір забезпечує досконале відтворення.

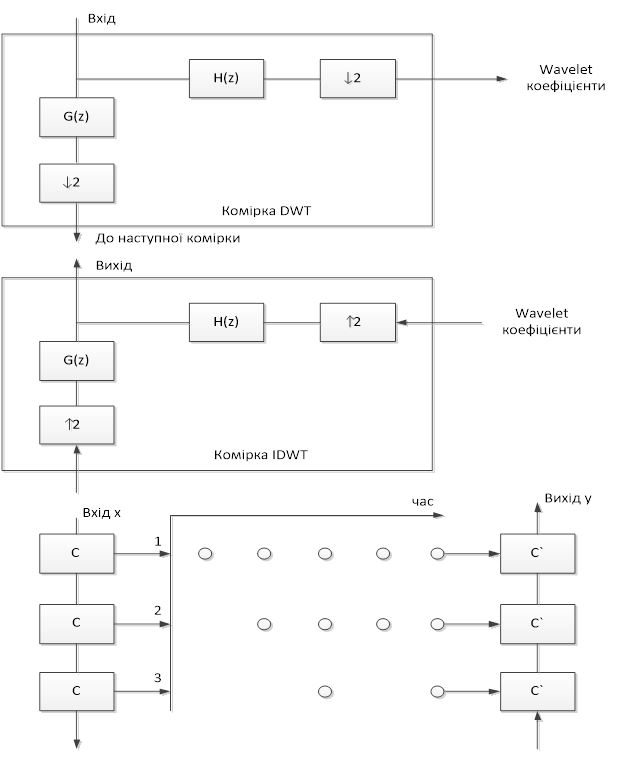
Рис. 2. Структура обчислень в DWT

2.Опис цифрових фільтрів

В алгоритмі DWT перетворення використовуються цифрові фільтри: h-фільтр високої частоти, g- фільтр низької частоти. Фільтри перекурсивні. Властивість пере курсивного фільтра полягає в тому, що вхідний сигнал фільтра залежить тільки від значення вхідного сигнала, на відміну від рекурсивного, в якому залежить від попередніх значень вхідного сигналу. Нерекурсивний фільтр при відсутності зворотнього зв’язку не можна розкачати. Він завжди стабільний. 

При синтезі не рекурсивного фільтра постає завдання визначити вагові коефіцієнти ак так, щоб задана бажана передаточна функція «по можливості» добре досягалася. Коефіцієнт ак – коефіцієнт передаточної функції. Передаточна функція визначається як відношення періодичних вхідного та вихідного сигналів. Це має місце також у цифрових системах. Таким чином, передаточну дискретну функцію цифрового фільтра можна отримати, якщо стимулювати його дискретним періодичним сигналом:

  

Дістаємо вхідний сигнал:

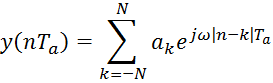
З нього обчислюється передаточна функція:

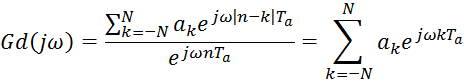
Передаточна функція буде добре досягатись, якщо апроксимація бажаної передаточної функції виконується за методом найменших квадратів. Для визначення коефіцієнтів необхідно виконати ряд кроків:

Скачать файл