Государственный комитет Российской Федерации по высшему образованию
Саратовский ордена Трудового Красного знамени
государственный технический университет
Методические указания
к лабораторной работе по курсу
“Теория управления” для студентов
специальности 2101
Одобрено
редакционно –издательским советом
Саратовского государственного
технического университета
Саратов
1999
Краткаятеория
Устойчивость линейных систем автоматического управления может быть определена по целому ряду критериев: Рауса, Гурвица, Михайлова, Найквиста.
Все перечисленные критерии предполагают знание дифференциального уравнения системы, всех его коэффициентов, структурной схемы. В ряде случаев описание системы (или ее части) дифференциальным уравнением бывает затруднительно или невозможно. Тогда применение упомянутых критериев становится невозможно.
В такой ситуации исследование устойчивости возможно экспериментально или на модели САУ. Исследование устойчивости на модели имеет ряд преимуществ. Модель допускает изменение параметров системы в широких пределах. При изменении параметров может быть определена область устойчивости, ее границы. Кроме того, может быть снят переходный процесс в системе, определены показатели качества управления и выбраны оптимальные показатели.
Таким образом, исследование САУ на модели дает дополнительные возможности, дополняет теоретические методы практическими, позволяет подтвердить или опровергнуть спроектированную САУ.
Модель САУ может быть реализована разными способами, в разных физических средах. В частности, модель может быть выполнена на аналоговой вычислительной машине, например на АВК-32.
В данной лабораторной работе исследуется система управления, допускающая анализ по уравнению и на модели. Результаты исследования двумя методами необходимо сравнить.
Пусть система управления задана следующей структурной схемой:

Рис. 1
Передаточная функция разомкнутой цепи такой САУ
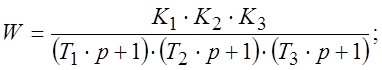 (1)
(1)
Необходимо упростить знаменатель выражения (1)
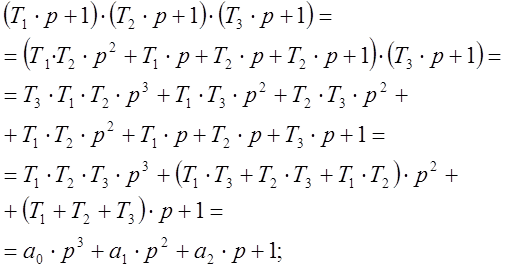 (2)
(2)
где Т1·Т2·Т3=а0; Т1·Т3+Т2·Т3+Т1·Т2=а1; Т1+Т2+Т3=а2.
Для замкнутой системы с учетом (2)
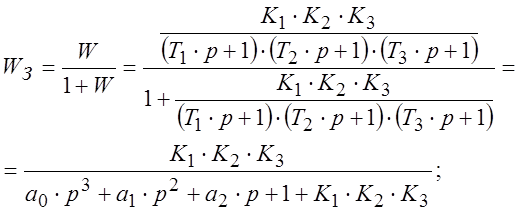 (3)
(3)
Характеристическое уравнение замкнутой системы:
D(p)=a0·p3+a1·p2+1+К1·К2·К3, (4)
где 1+К1·К2·К3=а3, а К1·К2·К3 - есть общий коэффициент передачи разомкнутой системы.
По критерию Гурвица все определители Гурвица должны быть положительны. Определитель Гурвица имеет вид:
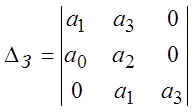
Тогда условие устойчивости
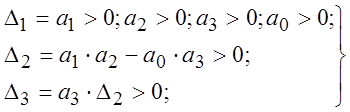 (5)
(5)
С учетом значения коэффициентов условие (5) имеет вид:
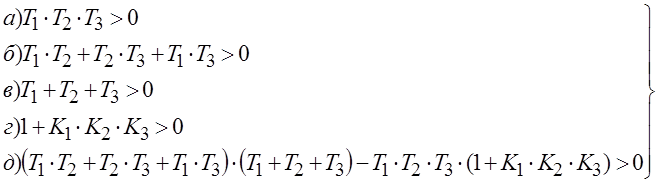
![]() (6)
(6)
Так как физически параметры Т1, Т2,Т3 всегда положительны, то устойчивость системы определяется выражениями (6 г) и (6 д). Система управления оказывается на границе устойчивости, если условия(6 г) и (6 д)становятся равенствами. Все параметры, соответствующие границе устойчивости, называются критическими и обозначаются Ккр, Т1 кр, Т2 кр и т.д. Влияние всех параметров на устойчивость системы одновременно изучить затруднительно. Графически наглядным является анализ устойчивости на плоскости каких-либо двух параметров, например Т1 и К=К1·К2·К3.
Тогда из (6 г) следует: К>-1, а Ккр=-1, (7)
а из (6 д) Т1·Т2·Т3·(1+K)>(Т1·Т2+Т2·Т3+Т1·Т3) (Т1+Т2+Т3),
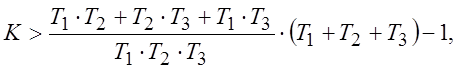 а
а
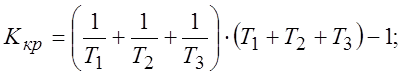 (8)
(8)
Т.к. варьируется только Т1, а Т2 и Т3 постоянны, то
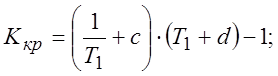 (9)
(9)
где 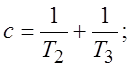 (10)
(10)
а ![]() (11)
(11)
Задаваясь значениями Т1 от 0 до ∞ можно получить кривую Ккр=f(Т1) по выражению (9)
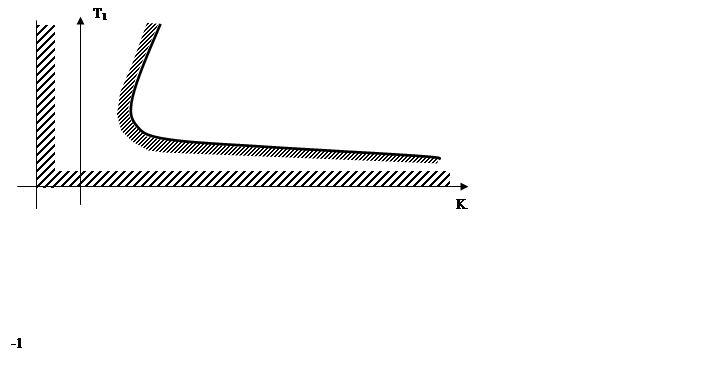 |
Рис. 2
Структурная схема заданной системы управления описана в наиболее общем виде. Для реализации модели системы управления на АВК-32 необходимо перейти к описанию, удобному для набора в аналоговых машинах.
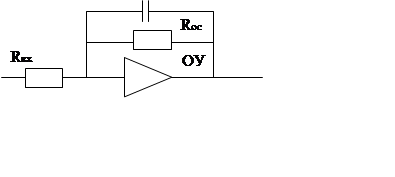 Ранее
была рассмотрена реализация апериодического звена с передаточной функцией К/(Т·р+1)
на базе блока БИ-31 в следующем виде:
Ранее
была рассмотрена реализация апериодического звена с передаточной функцией К/(Т·р+1)
на базе блока БИ-31 в следующем виде:
|
||||
|
||||
Рис. 3
Здесь Т=Rос·Сос, а К=Rос/Rвх.
Набор звена выполняется соединением свободного гнезда одного из входных резисторов блока с выходом усилителя и включением выбранного конденсатора в интегратор соединением его свободного входа на наборном поле с гнездом "^".
Учитывая, что в заданной системе управления, апериодических звеньев три, описанную операцию набора необходимо повторить три раза.
При наборе каждого звена необходимо выполнить проверку его функционирования в статическом режиме. Для этого на вход звена подается фиксированное напряжение. Напряжение на выходе звена измеряется вольтметром (цифровым или стрелочным). По окончании переходного процесса определить коэффициент передачи k как отношение Uвых/Uвх и сравнить с заданным через отношение Rос/Rвх.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.