Федеральное агентство по образованию
Южно-Уральский Государственный Университет
Кафедра радиотехнических систем
Лабораторная работа №2
Исследование устойчивости и коррекция линейных САУ.
Выполнили: студенту гр. ПС-450
Кириллов В.В.
Гребенщиков И.Ю.
Байда М.А.
Проверил: Баландин А.В.
Челябинск 2009
Цель работы: Получение навыков применения критериев устойчивости для исследования устойчивости систем автоматического управления с использованием пакетов программ для моделирования систем управления. Ознакомление с методикой построения корневых годографов для анализа и синтеза линейных (линеаризованных) систем автоматического управления.
Выполнение работы.
Структурная схема:
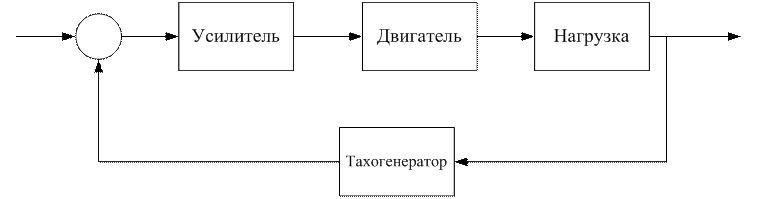
Передаточная функция нагрузки:
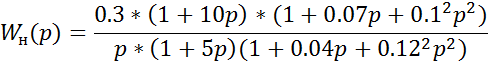
Передаточная функция системы:
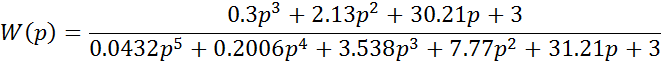
Характеристическое уравнение имеет вид:
![]()
По критерию Льенара-Шипара для устойчивости САУ, необходимо и достаточно, чтобы выполнялось необходимое условие устойчивости и чтобы при четном (нечетном) порядке характеристического полинома определители Гурвица нечетных (четных) порядков были положительны.
Из характеристического уравнения видно, что выполняется необходимое условие устойчивости
(![]() )
)
Матрица Гурвица:
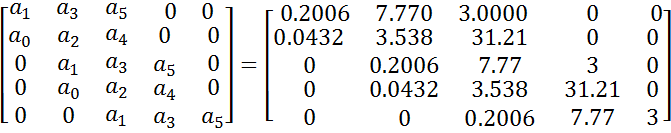
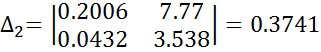 >0
>0
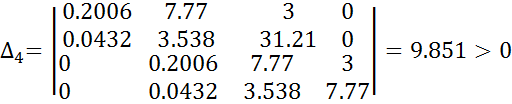
Критерий Льенара-Шипара выполняется, следовательно САУ устойчива.
Критерий Найквиста:
Для того, чтобы замкнутая система, неустойчивая в разомкнутом состоянии, была
устойчива необходима и достаточно, чтобы годограф частотной передаточной
функции разомкнутой системы при возрастании ![]() от
0 до
от
0 до ![]() охватывал точку (-1;0)
в положительном направлении ровно R/2
раз, где R- число неустойчивых
полюсов.
охватывал точку (-1;0)
в положительном направлении ровно R/2
раз, где R- число неустойчивых
полюсов.
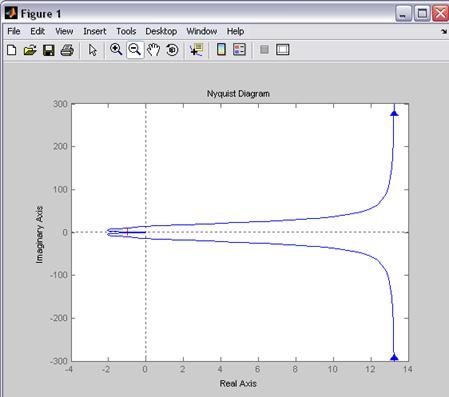
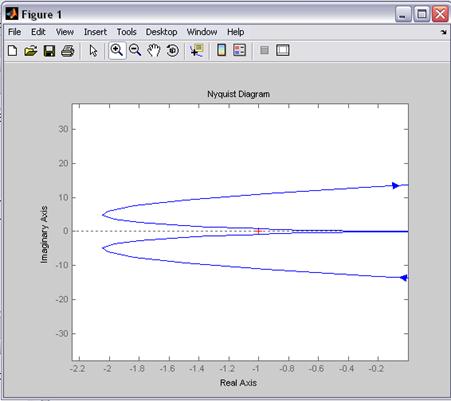
Критерий выполняется, следовательно система устойчива.
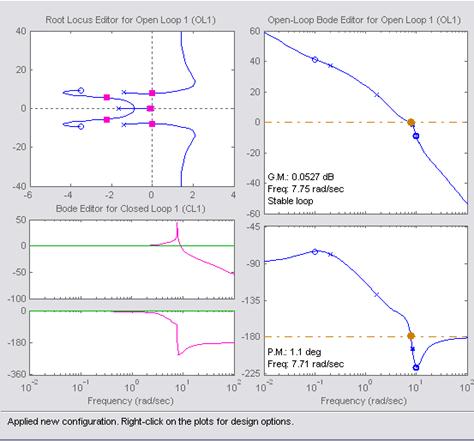
Находим запас устойчивости по фазе и амплитуде
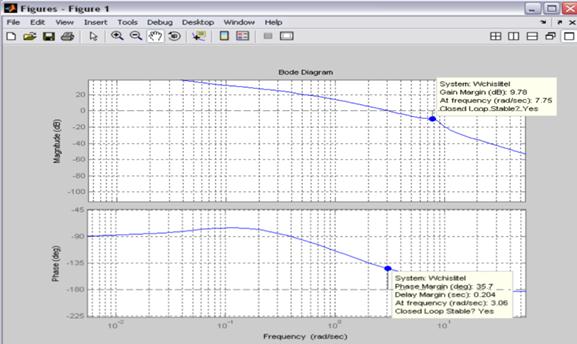
Из
графиков видно, что на частоте среза ![]() запас устойчивости по
фазе равен
запас устойчивости по
фазе равен ![]() .
.
На
критической частоте ![]() запас устойчивости по
амплитуде равен
запас устойчивости по
амплитуде равен ![]() .
.
Значения полюсов и нулей разомкнутой системы:
Zero(Wраз.) ans = -0.1000; -3.5000 + 9.3675i; -3.5000 - 9.3675i;
pole(Wраз.) ans = 0; -0.2000; -1.6669; -1.3883 + 8.2164i; -1.3883 - 8.2164i;
Корневой годограф замкнутой системы имеет вид:
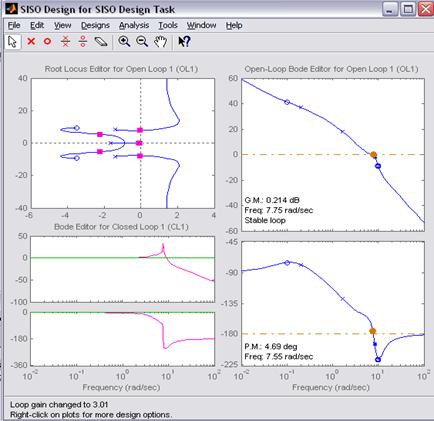
Из корневого годографа видно, что САУ устойчивая, так как все корни характеристического уравнения расположены в левой полуплоскости.
Определение условия неустойчивости системы.
Определим ![]() для нахождения границы
устойчивости.
для нахождения границы
устойчивости.
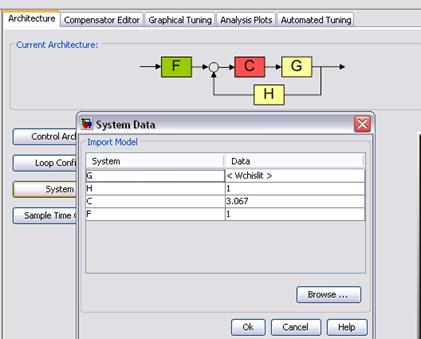
Где Wchislit=Wn*Wdv*Wusil
![]()
![]()
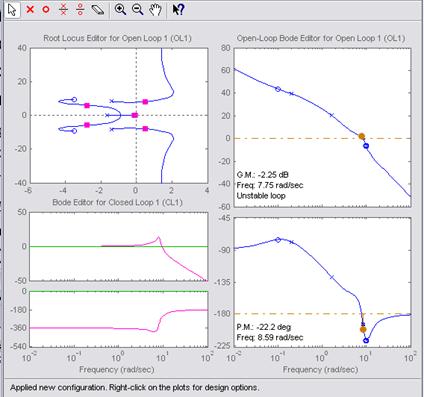
При
увеличении значения ![]() САУ потеряет
устойчивость.
САУ потеряет
устойчивость.
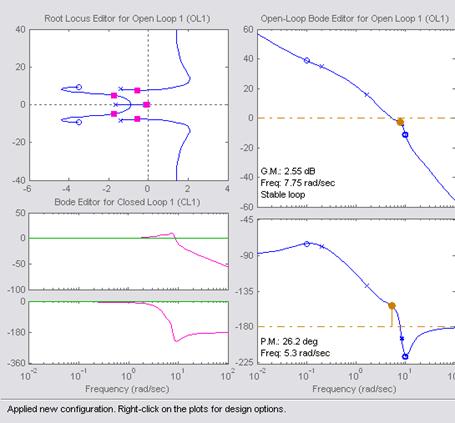
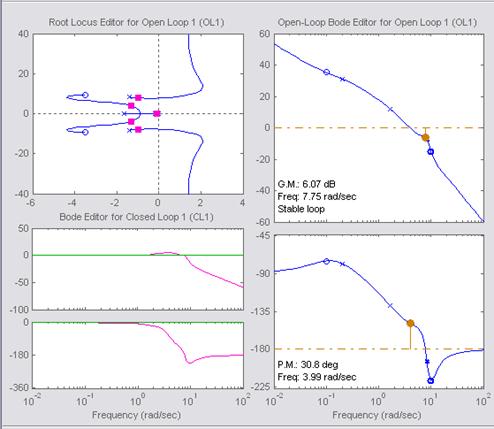
Исследуем
переходные и частотные характеристики для различных значений ![]()
![]()
![]()
![]()
![]()
![]()
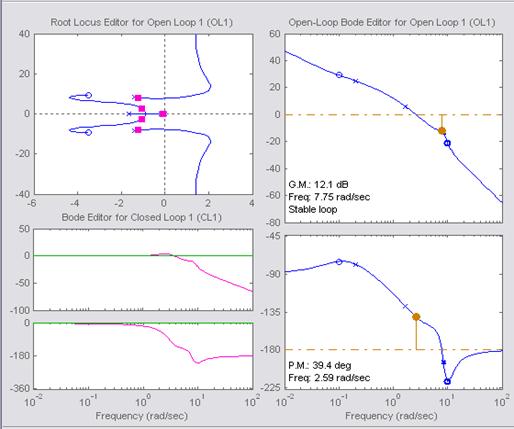
Выберем желаемое поведение системы, отличающееся от исследуемой системы, превосходящее его по перерегулированию.
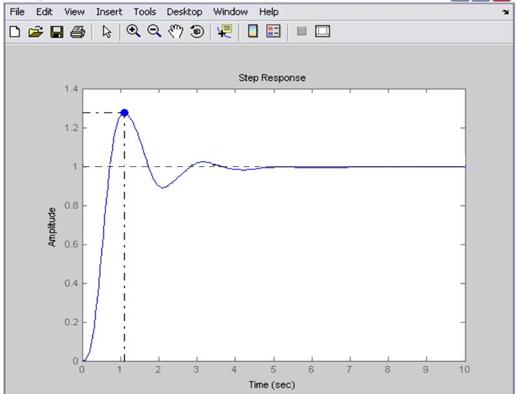
Передаточную функцию корректирующего звена определим по формуле:
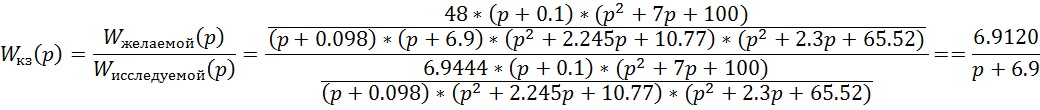
Где 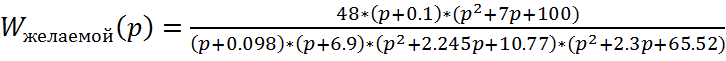
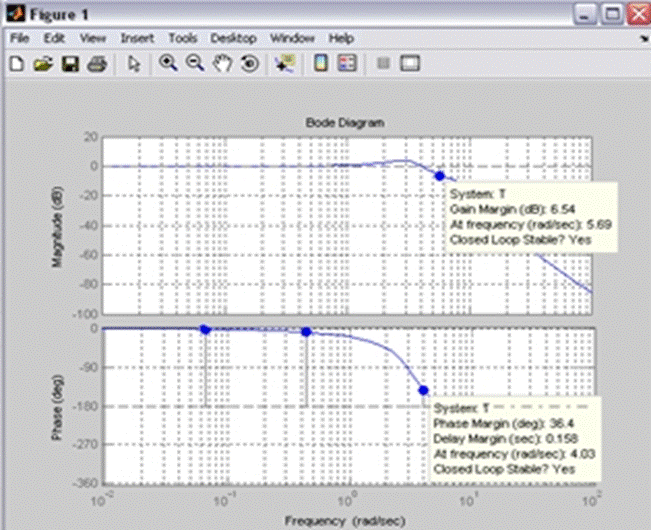
Как видно из графика логарифмических частотных
характеристик желаемой передаточной функции запас устойчивости по фазе равен ![]() , что на
, что на ![]() больше
чем у исследуемой, запас устойчивости по амплитуде равен
больше
чем у исследуемой, запас устойчивости по амплитуде равен ![]() , что на 3,24 меньше
чем у исследуемой системы.
, что на 3,24 меньше
чем у исследуемой системы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.