Теория автоматического регулирования, страница 4

Х1 – сигнал на выходе основного источника

Х2 – сигнал на выходе нагрузки (регулируемая величина)

Х6 – сигнал на выходе исполнительного механизма

Х8 – сигнал на выходе уставки

Данные результаты нас не устраивают, так как ЭДС регулируемого источника в установившемся режиме не равна нулю, а регулируемая величина не равна уставке. Следовательно, структурно-алгоритмическая  схема нашей системы нуждается в корректировке.

11.  Корректировка и расчёт основных параметров системы

Выбрать значения коэффициентов К_ри К_д из области устойчивости, которые в статическом режиме обеспечивают нулевую величину ЭДС Е_р регулируемого источника. По результатам эксперимента рассчитать статизм и для выбранных значений коэффициентов К_ри К_д. Рассчитать теоретические значения указанных показателей.

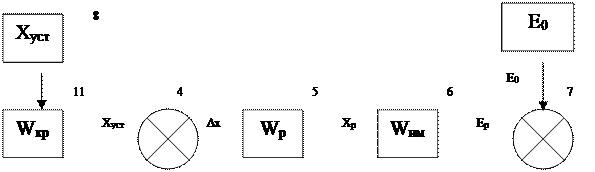
Причиной некорректной работы системы, проиллюстрированной в п. 10, является несогласованность схемы сравнения регулируемой величины с уставкой: датчик ослабляет в 10 раз (Кd = 0.1) сигнал с выхода нагрузки, а уставка выдаёт сигнал той величины, которой должен быть сигнал на выходе нагрузки. В результате на исполнительный механизм поступает ложный сигнал рассогласования и система работает неправильно. Это можно исправить введением после уставки пропорционального звена, коэффициент передачи которого будет равен коэффициенту передачи датчика:

					1
									х

 

                     

 

Промоделируем процесс в скорректированной системе с теми же величинами Кd = 0.1 и

Кр = 10:

Х1 – сигнал на выходе основного источника

Х2 – сигнал на выходе нагрузки (регулируемая величина)

Х6 – сигнал на выходе исполнительного механизма

Х8 – сигнал на выходе уставки

Как видно по результатам проведённого опыта, мы смогли добиться нулевой ЭДС регулируемого источника и равенства регулируемой величины уставке в установившемся режиме.

Рассчитаем теоретические значения параметров системы:

1). Статизм

2). Перерегулирование

a₀ = 287; a₁ = 27.22*10³; a₂ = 82.96*10⁴; a₃ = 4.1152*10⁶ К_р К_д+8*10⁶

3). Длительность переходного процесса

Экспериментальные статизм, перерегулирование и длительность переходного процесса можно найти из опыта п. 12, в котором имитируется потеря 50 % ЭДС, т. е. изменение воздействия, что и требуется для опытного вычисления статизма.

12.  Моделирование аварийного режима работы САУ

Подготовить имитационную модель, позволяющую за один расчет выполнить:

—  моделирование процесса включения системы питания с получением установившегося режима;

— моделирование последующего переходного процесса, обусловленного потерей 50% величины э.д.с. Е₀с получением нового установившегося режима.

Воспользуемся имитационной моделью, приведённой в п. 10 с учётом внесённой в п. 11 корректировки. Значения коэффициентов Кр и Кd прежние (Кd = 0.1 и Кр = 10).Для имитации аварийного режима зададим потерю 50 % величины ЭДС основного источника в момент времени t = 1 с:

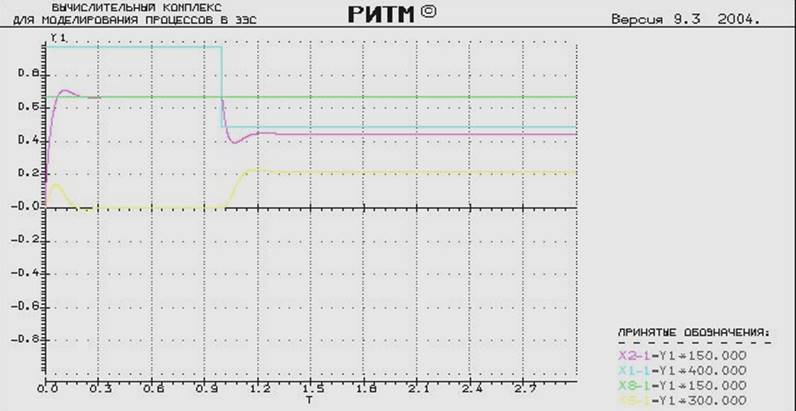
Х1 – сигнал на выходе основного источника

Х2 – сигнал на выходе нагрузки (регулируемая величина)

Х6 – сигнал на выходе исполнительного механизма

Х8 – сигнал на выходе уставки

Опытные характеристики:

1). Статизм

2). Перерегулирование

3). Длительность переходного процесса – 0.3 сек.

Отличие теоретических и опытных параметров составило не более 18 % (перерегулирование), менее 0.01 % (статизм) и не более 10 % (длительность переходного процесса).

13.  Оптимизация САУ

Провести поэтапную оптимизацию коэффициентов К_ри К_д с целью обеспечения допустимых значений показателей качества.

Технологические требования:

1). Статизм – не более 5 %

2). Перерегулирование – не более 30 %

3). Цепи регулирования  системы должны быть низковольтными