Привод звена промышленного робота (нижней руки). Типовой технологический процесс и выбор манипулятора, страница 8

Результатом расчета переходных процессов являются зависимости угловой скорости и момента от времени, т.е. ω(t) и M(t). В ряде случаев задается по закону

ω₀(t)=ω_0нач+ε₀t, где ω_0нач-заданная угловая скорость при t=0;

ε₀-заданное значение углового ускорения(замедления или ускорения).

В этом случае действительная угловая скорость двигателя рассчитывается следующим образом[6]:

ω=ε₀t+( ω_0нач-∆ω_ст-ε₀Т_м)(1-)+ω_нач, где ∆ω_ст-статическое падение скорости двигателя:

ω_нач-начальная скорость двигателя.

Статическое падение угловой скорости двигателя можно найти через жесткость механической характеристики:

∆ω_ст=, где -постоянный статический момент на рабочих участках технологического цикла.

Так как в нашем случае М_ст=М_уст=3,13 Н*м, то по формуле (4.26) получаем:

∆ω_ст==60,60(рад/с).

Электромагнитный момент двигателя определяется выражением:

М=М_ст+Jε₀+(М_нач-М_ст- Jε₀), где М_нач- начальное значение электромагнитного момента двигателя .

Для передней руки момент сопротивления определяется только активным статическим моментом. Поэтому будем использовать формулы для пуска и торможения двигателя при активном статическом моменте.

Начнем с пуска при активном статическом моменте. На интервале времени 0<t<t₀, где t₀-заданное время пуска, имеем:

ω=ε₀t-(∆ω_ст+ε₀Т_м)(1-),

М=М_ст+Jε₀(1-)- М_ст  

На интервале t₀<t<t_п+3Т_м:

ω=ω_0кон-∆ω_ст-ε₀Т_м, где ω_0кон-конечное значение заданной угловой скорости;

М=М_ст+Jε₀.

Торможение при активном статическом моменте. На интервале времени 0<t<t₀, где t₀-уже заданное время торможения имеем:

ω= ω_0нач-∆ω_ст- ε₀t+ε₀Т_м)(1-),

М=М_ст-Jε₀.

На интервале t₀<t<t₀+3T_м:

ω= -∆ω_ст+ε₀Т_м,

М=М_ст-Jε₀.

Абсолютное значение заданного углового ускорения как для пуска (t₀=t_п, ω_0кон=ω_уст), так как и для торможения(t₀=t_т, ω_0нач=ω_уст) двигателя выразим следующим образом:

ε₀=;

ε₀==104.72(рад/с²).

Подставив все известные величины в формулы(4.28)-(4.35), получим следующие переходные переходные характеристики:

а) для пуска:

ω(t)=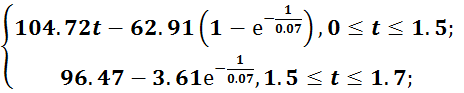  

M(t)=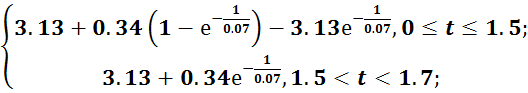 б) для торможения:

ω(t)=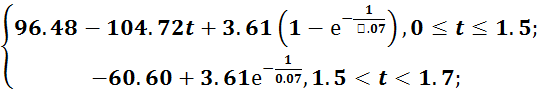         

M(t)=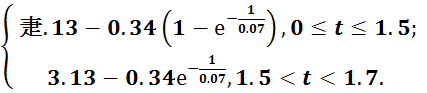 

Графики зависимостей (4.38)-(4.40) изображены на рисунках 4.2, 4.3.

В целом на рисунках механические переходные процессы имеют типичный для пуска и торможения вид. Но есть принципиальные отличия- это наблюдается во время пуска при t(0,9;0,6) для зависимости ω(t) и во время торможения при t(0,9;1,6) для зависимостей ω(t), M(t). Эти отличия объясняются тем, что формулы для расчета переходных процессов не учитывают принятых ещё в разделе 2 допущений.

Так, в действительности при остановке ЭД передняя рука не будет двигаться самостоятельно под действием силы тяжести из-за редуктора с большим передаточным числом(i=255.4).

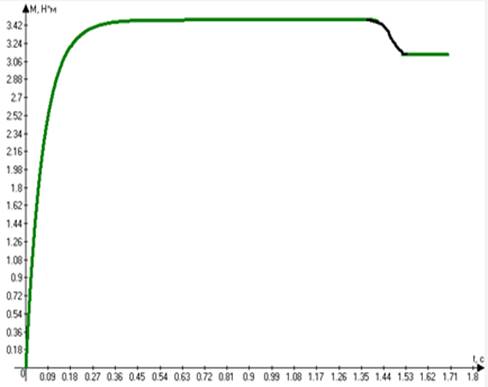
Рис.

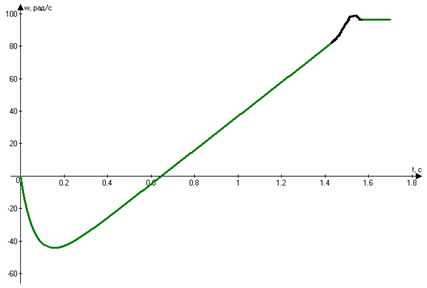
Рисунок 4.2-Механические переходные процессы в ЭП при пуске

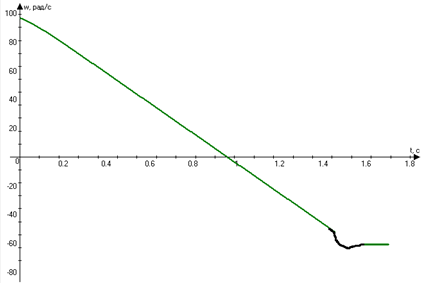
Рис.

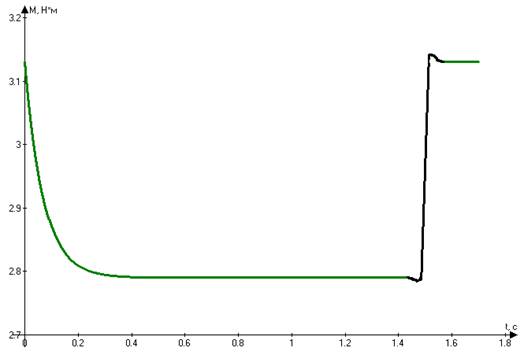
Рисунок 4.3-Механические переходные процессы в ЭП при торможении

Время окончания переходного процесса для рассмотренных зависимостей брали, считая двигатель апериодическим звеном 1-го порядка(t₀+3T_м=1,7 с.). Обычно для апериодического звена по истечении указанного времени, отклонения скорости и момента от установившихся значений составляют не более 5%. В данном случае, как видим, это не совсем так ввиду принятых допущений.

s==;

s==0,31 или 31%.

Такое большое значение статизма объясняется, как разомкнутой структурой ЭП, так и тем, что двигатель работает по искусственной механической характеристике со скоростью идеального ХХ, меньшей в 2 раза, чем аналогичная скорость для естественной характеристики.

Разомкнутый ЭП данного проекта не подходит для регулируемых приводов станков и ПР: так максимально допустимое значение статической ошибки регулируемого ЭП для диапазона регулирования 100 составляет 5%[7]. Эта проблема решается построением замкнутых структур ЭП, что будет рассмотрено в следующем разделе.

Размещено на