Привод звена промышленного робота (нижней руки). Типовой технологический процесс и выбор манипулятора, страница 7

ω_нач=ω_сред∆ω,

∆t_собс=∆∆t,

М_дин’=’∆ М_дин’,

Jмех=∆J,

Где средние величины определяются как:

А_ср=,

а отклонения:

∆А=.

Тогда точность остановки выражается следующим образом:

∆φ_т=ω_ср∆t_ср.

Наибольшее влияние на неточность остановки оказывает средняя остановочная скорость ω_ср. Поэтому, подставив в (4.14) допускаемую неточность позиционирования  и решив уравнение относительно ω_ср, можно найти:

ω_ср=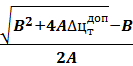, где введены следующие величины:

A=,

B=t_ср, где в свою очередь, -среднее угловое ускорение передней руки.

Для расчета остановочной пониженной скорости ω_ср задаются следующими параметрами:

=0,2…0,5-чем меньше значение, тем выше жесткость механических характеристик;

=0,1…1,15;

=0,2…0,3 с.

Принимаем для средней жесткости =0,3, а-=1;=0,3 с.

Предельные значения динамического момента определяются по формулам:

=М_т+,

=М_т+.

Где М_т-момент механического тормоза;

, -предельные значения момента статического усилия.

Максимальные значения статического момента будет =678,48 Н*м при угле поворота передней руки φ=0. Минимальное значение  Н*м при угле φ=65(см.раздел 2.3).

Так как в проектируемом ЭП торможение осуществляется электрическим методом- противовключением, то механический тормоз попросту отсутствует и M_т=0. Значит по формулам (4.18), (4.19), (4.12), (4.13) имеем:

==678,48 Н*м;

==286,74 Н*м;

=(678,48+286,74)/2=482,61(Н*м);

=(678,48-286,74)/2=195,84(Н*м);

=195,87/482,61=0,406.

Максимальный момент инерции производственного механизма был ранее уже определен при рассмотрении случая, когда передняя и верхняя руки расположены по одной прямой(см.подраздел 2.1), =J_мех=90,65 кг*м².

Минимальный момент инерции производственного механизма найдем для случая, когда верхняя рука максимально прижата к передней руке. Преобразуем формулу(2.2) и воспользуемся формулами (4.12), (4.13):

J_мех=m₂/12+m₃/3(l’₂+l’₃/2)²+m_г/3(l’₂+l’₃)²

=43.5*2.4/12+14(1.55-0.25)²/3+5(1.55-0.5)²/3=8.7+7.8+1.75=18.25(кг*м²);

=(90,65+18,25)/2=54,45(кг*м²)

∆J=(90.25-56.95)/2=16.65 (кг*м²)

Среднее значение углового ускорения найдем следующим образом[6]:

ε_ср=,

ε_ср==8.86 (рад/с²)

Теперь вернемся к формулам (4.15), (4.16), (4.17) и получим:

А=1/2*8,86(2*0,3+0,3+0,4)=0,07;

B=0,3(0,3+1)=0,39;

ω_ср==0,007(рад/с).

Зная максимальную угловую скорость передней руки, можно вычислить допустимый диапазон регулирования скорости ЭП[7]:

D=;

D=0.615/0.007=87.85.

Далее будем ориентироваться на стандартное значение диапазона регулирования 100. Оно понадобится нам для выбора комплектного ЭП.

4.3 Расчет и анализ переходных процессов

Переходные процессы в ЭП, как и в разомкнутой системе, рассчитывают за цикл нагрузочной диаграммы. Методика расчета зависит от системы ЭП, вида механической характеристики двигателя, характера статического момента, учета постоянных времени [6].

Примем для нашего случая следующие допущения:

-ЭП представляем как одномассовую систему;

-управляющее воздействие изменяется линейно, что характерно системам типа «управляющий преобразователь-жвигатель»;

-моменты сопротивления представлены только активными моментами.

Характер переходного процесса зависит от инерционностей ЭП (электромеханической Т_м и электромагнитной Т_э постоянных времени двигателя) и их количественного соотношения.

Электромеханическая постоянная времени ДПТ с линейной механической характеристикой [6]:

Т_м=, где J-суммарный, приведенный к валу двигателя, момент инерции ЭП;

Т_м==6,98*10^-2 (с).

Электромагнитная постоянная времени цепи якоря двигателя:

Т_э=;

Т_э==5,14*10^-4(с).

Так как Тм намного больше Тэ, то можно вместо электромеханического рассматривать только механический переходной процесс, обусловленный механической инерцией.