Задать переключательную функцию (ПФ) – значит указать ее значение при всех возможных комбинациях (наборах) значений его аргументов. Логические и переключательные функции могут иметь различные формы представления: словесную, табличную, алгебраическую, графическую. Самым простым и наглядным является табличный способ задания. При этом способе составляется таблица с указанием всех наборов аргументов и значений функций для каждого из них. Эта таблица называется таблицей истинности или таблицей соответствия. Кроме наглядности, табличный способ обладает тем достоинством, что каждой функции соответствует одна и только одна таблица истинности и наоборот. Недостаток табличного способа – громоздкость таблицы истинности, которая растет с ростом числа переменных. Кроме того, эта форма при всей ее наглядности не позволяет выяснить каким образом следует реализовать данную функцию и как ее упростить. Аналитический способ (алгебраический) - для реализации и последнего упрощения ПФ, т.е. записать ее в виде некоторой формулы. Однако одну и ту же переключательную функцию можно в принципе представить различными аналитическими выражениями. Доказано, что применительно основному функционально-полному набору ПФ, содержащему элементы или операции конъюнкцию, дизъюнкцию и инверсии. Любая ПФ, предварительно заданная в табличном виде может быть записана аналитически в двух формах, называемых каноническими (нормальными): ДСНФ (дизъюнктивная совершенная нормальная форма); СКНФ (конъюнктивная совершенная нормальная форма). Аналитическая запись ПФ в ДСНФ и КСНФ строится по средствам суперпозиции (наложения) специальных вспомогательных функций минтермов mi и макстермов Мi.
(8)Понятие о минтермах и макстермах
Минтерм mi – булево произведение (конъюнкция) от n переменных, в котором каждая переменная входит только 1 раз,
в прямом или инверсном виде. Макстерм Мi – элементарная
дизъюнкция. Представляет собой булеву сумму от n
переменных, в которой каждая переменная входит 1 раз в прямом или инверсном
виде. Любая ПФ от n-переменных имеет по 2n минтермов и макстермов, т.е. их
число равно числу наборов, на которых она представлена. Любая ПФ в общем случае
может быть представлена в виде СДНФ: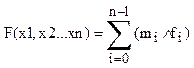 
, СКНФ: 
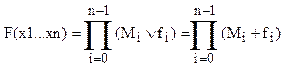, где fi – значение функции на i-том
наборе переменных. Любая ПФ, заданная таблично, может быть представлена в виде
СДНФ и СКНФ, которые эквивалентны. Выбор формы представления зависит от числа
наборов аргументов, на котором функция равна 1 – СДНФ либо равно 0 – СКНФ, но
при минимизации функций более удобной является запись в форме СДНФ. Обратный
переход выполняется путем последовательной подстановки в формулу всех возможных
наборов переменных, нахождение значений функций на этих наборах и затем
заполняем таблицу истинности.
(9)Графическое представление ПФ. Карта Карно
Графический способ – при относительно малых (n≤6) переменных – карты минтерма или Карно. Карта Карно содержит q=2n клеток, причем каждой клетке соответствует один из q минтермов. На практике безразличными являются такие наборы переменных, которые при работе соответствующего устройства никогда не реализуются.
(10)Минимизации ПФ и ее смысл
Законы алгебры логики позволяют получать для каждой ПФ множество эквивалентных представлений. Чем проще выражение для функции, тем меньше элементов требуется для ее технической реализации. Сложность функции определяется количеством переменных, входящих в ее алгебраическое выражение. В теоретических разработках сложность записи функции в ДНФ оценивают по методу Квайна. Сомножитель под знаком инверсии оценивается 2 единицы. Полная цена ПФ определяется путем подсчета общего количества сомножителей в конъюнкциях и прибавления их к полученному значению количества этих конъюнкций. Под минимизацией ПФ подразумевает нахождение для нее такой ДНФормы, которая имеет min цену (стоимость). Решение, обобщенное задачей минимизации с целью получения схем min денежной стоимости. Наиболее часто процесс минимизации просматривается в упрощенной установке, как можно меньше число переменных.
(11)Методы минимизации ПФ
В настоящее время предложено несколько методов минимизации ПФ. Все они основаны на преобразованиях логических выражений и подразделяются на систематические и несистематические. Систематические методы: достоинство – этих методов является возможность их полной формализации, т.е. они могут быть описаны строгими алгоритмами. Поэтому многие из них реализованы в виде стандартных программ для ЭВМ. К числу наиболее распространенных систематических методов относится метод Квайна-Маккласки.
(12)Метод Квайна-Маккласки нахождения минимальных форм ПФ
Нахождение min формы ПФ по этому методу осуществляется в 3 этапа: анализируется вид задания ПФ. Если она задана в произвольной форме, то с помощью законов булевой алгебры она приводится к виду СДНФ. Нахождение сокращенной СДНФ. Ее ищем на основе операций склеивания и поглощения. Если в формуле ПФ присутствуют минтермы, отличные друг от друга формой вхождения только одной переменной, то такие минтермы называются смежными (соседними). Смежные минтермы отличаются друг от друга только одним аргументом, который входит в один минтерм прямой, а в другой в инверсной форме. Смежные минтермы могут быть попарно склеенными.
(13)Определение импликант, простые импликанты, избыточные импликанты
Результат склеивания соседних или смежных минтермов называется импликантой, которая представляет собой конъюнкцию, число аргументов в которой на 1 меньше, чем в исходном минтерме. Обычно в процессе минимизации сначала склеивают смежные минтермы, затем импликанты. Склеивание двух смежных импликант дает импликанту эквивалентную четырем минтермам. Такие импликанты называются простыми, состоящими из дизъюнкции простых импликант, называемых сокращенной ДНФ. Может оказаться, что в сокращенной ДНФ входят импликанты, наличие или отсутствие которых не сказывается на значение функции. Такие простые импликанты – избыточные.
(14)Тупиковые ДНФ и их значение для нахождения min форм ПФ
Если из сокращенной ДНФ удалить все избыточные импликанты, то получится ДНФ, которая называется тупиковой. Искомая min ДНФ совпадает с той из тупиковых ДНФ, которая содержит наименьшее число вхождений аргументов. В методе Квайна-Маккласке для получения тупиковых форм используется метод импликантных матриц. Импликантная матрица представляет собой таблицу, строки которой соответствуют минтермам, входящих в сокращенную СДНФ, а столбцы соответствуют простым импликантам или наоборот. С помощью импликантной матрицы удаляют все избыточные импликанты и получает min СДНФ. Этот метод хорошо реализуется программным путем на ЭВМ.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.