Информатизация общества и ее составляющие. Поколения ЭВМ и причины их смены. Классификация средств вычислительной техники. Область применения, типы ЭВМ и требования к ним, страница 3

(10)Представление чисел в форме с фиксированной запятой (точкой)

(11)Причины изменения разрядной сетки ЭВМ при вычислениях и их влияние на точность вычислений

(12)Представление чисел в форме с плавающей запятой (точкой), достоинства и недостатки такого представления

Числа изображаются с использованием как мантиссы так и порядка, поэтому в этих ЭВМ запись любого числа состоит из двух полей: 1)m_разр – для записи мантиссы М_А; 2)Р_разр – порядок Р 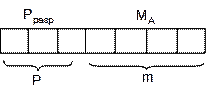. Т.к. основания СС для машины величина фиксированная, то для представления А=2^РМ_А надо знать только порядок Р. Представление любого числа А≠0 в общем случае является неоднозначным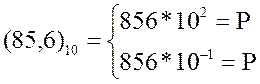. Для получения однозначного представления некоторого числа А в некоторой S – системе в форме с плавающей точкой порядок Р выбирается таким образом, чтобы М_А заключалась в диапазоне: S^-1≤M_A≤1. мантисса для каждого числа ≠0 должна быть нормирована. Мантисса должна быть правильной дробью, у которой а_-1≠0. как видно из рассмотренного примера 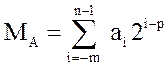, А=2^рМ_А=2^рΣa_i2^i-p, МА=а_-1а_-2…а_-m, 1≤М_А≤1-2^-ℓ. Основное преимущество представления чисел с плавающей точкой в сетке порядка 30-32 клеток не возникает проблем с нормированием мантиссы. В современных микропроцессорах обеспечивается представление данных Amin≤A≤Amax. Amin=10^-306; Amax=10⁺³⁰⁶. очевидно, что данный диапазон включает в себя практически все возможные числовые значения, которые могут встречаться при решении практических и научно-технических задач. Относительная погрешность: Аист=А±ΔА. 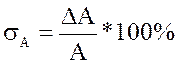. Для ЧПТ существенно меньше, чем для чисел с фиксированной точкой. Потеря производительности для ЧПТ обусловлена необходимостью работы с мантиссой, так и с порядком.

(13)Представление чисел в ЭВМ в двоично-десятичной форме

При обработке больших массивов десятичных чисел проходится тратить много времени для перевода этих данных в двоичную систему счисления. Чтобы обработать эти данные в ЭВМ, а затем выполнить обратный перевод полученных данных. Если включить в состав ЭВМ специальные функциональные блоки, или сопроцессоры десятичной арифметики, то появляется возможность обрабатывать десятичные числа напрямую, что сокращает время вычислений, при этом каждая десятичная цифра представляется двоичной тетрадой.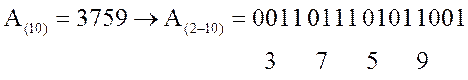. значение знака числа отличается специальным кодом. ,,+,, - ,,1100,,; ,,-,, - ,,1101,,.

(14)Арифметические действия над числами в ЭВМ

Современные ЭВМ имеют достаточно развитую систему команд, включающую от 10 до 100 машинных операций, при этом выполнение любой операции может быть сведено использованием простейших микроопераций типа: сложение и сдвига, что позволяет иметь универсальное арифметико-логическое устройство для выполнения любых операций, связанных с обработкой информации. Во всех ЭВМ все операции выполняются над числами, представленными специальными машинными кодами. При этом для обработки алгебраических величин, чтобы исключить трудности, связанные с необходимостью учета знаков, знаковых разрядов алгебраические величины отображают на счетное упорядоченное множество положительных чисел. В зависимости от способа такого отображения различают следующие виды машинных кодов чисел: прямой код ПК, дополнительный код ДК, обратный код ОК. применение этих кодов позволяет использовать и обрабатывать знаковые разряды чисел также как и числовые значения, а также заменять операцию вычитания сложением. В настоящее время ОК применяются сравнительно редко, и представляю больше теоретический интерес. ПК двоичного числа образуется из абсолютного значения и знака. А=±|А|, ,,+,, - 0, ,,-,, - 1. ОК для положительных чисел совпадает с их ПК, а ОК отрицательных чисел имеет 1 в знаковом разряде, а значащие разряды числа заменяются инверсными. А=10101, ГА=01010=Ā. Недостаток ОК то, что в них 0 может быть как положительным, так и отрицательным. Такая неоднородность явилась причиной того, что в современных ЭВМ используется ДК. ДК положительного числа совпадает с ПК. ДК отрицательного числа представляет собой результат суммирования ОК этого числа со значением единицы младшего разряда. ДК получил свое название в связи с тем, что представление отрицательных чисел является дополнением ПК числа до машинной единицы. При этом сложение ДК положительного числа с его отрицательным значением дает машинную единицу. Чаще всего используют модифицированные ДК и ОК, отличающиеся от обычных ДК и ОК тем, что имеют удвоенный знак разряда:,,+,,→,,00,,; ,,-,,→,,11,,. Это делается для того, чтобы исключить получение неправильного результата в слечае возможного переполнения разрядной сетки влево. Значение знакового разряда типа ,,01,, говорит о положительном переполнении разряда сетки, а ,,10,, - об отрицательном переполнении.

Арифметические операции на ЧФТ

Сложение двоичных чисел в ЭВМ осуществляется последовательно и по разрядам. При этом должны соблюдаться следующие правила: 1)слагаемые должны иметь одинаковое число разрядов. Для выравнивания разрядной сетки могут быть записаны незначащие нули слева в целой части числа и незначащие нули справа в дробной части числа; 2)знаковые разряды участвуют в сложении так же, как и значащие разряды; 3)преобразование кодов чисел производится с учетом знака. При этом незначащие нули изменяют свое значения по общим правилам; 4)при образовании единицы переноса в случае ОК, эта единица складывается с младшими числовым разрядом. При использовании ДК, единица теряется. Знак результата формируется автоматически, а сам  результат представляется в том коде, в котором были представлены исходные данные. Операция вычитания приводится к операции сложения путем преобразования чисел в ОК или ДК. Умножение двоичных чисел наиболее просто реализуется в ПК. Произведение получается путем сложения частных произведений, представляющих собой разряды множимого, сдвинутые влево в соответствии с позициями разрядов множителя. Частные произведения, полученные умножением на 0 игнорируются. Особенностью умножения n-разрядных сомножителей является увеличение разрядности до 2n. Знак произведения формируется путем сложения знаковых разрядов сомножителей. Возможные переносы из знаков разрядов игнорируются. Как и в 10ой арифметике деление является операцией умножения, но с учетом того, что все вычисления ЭВМ заменяются сложением обратных видов ДК, то в действительности операция деления приводится к операциям сложения и сдвигу вправо разрядов делителя относительно разрядов делимого. При этом  делимое должно быть приведено к 2-n разрядной сетке, поскольку только в этом случае при делении его на n-разрядный делитель получится n-разрядное частное. Знак частного формируется, как и при умножении.