Информатизация общества и ее составляющие. Поколения ЭВМ и причины их смены. Классификация средств вычислительной техники. Область применения, типы ЭВМ и требования к ним, страница 4

Арифметические операции над ЧПТ

В ЭВМ ЧПТ хранятся в памяти, имея мантиссу и порядок, представленные в ПК или нормализованном виде. Все арифметические действия над такими двоичными числами производятся как и с 10-ными, представленными в полулогарифмической форме. При чем порядок и мантисса образовываются отдельно. Сложение (вычитание) производится в след. последовательности: а)сравниваются порядки исходных чисел путем вычитания 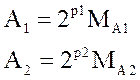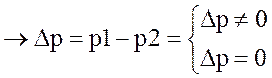. б) если , то это означает, что одноименные разряды мантисс имеют одинаковые веса (порядки); если , то необходимо произвести выравнивание порядков. в)для выравнивания порядков, число с меньшим порядком сдвигается вправо на . При этом младшие разряды выталкиваются из разрядной сетки и теряются. г)после выравнивания мантиссы можно складывать или вычитать. Операция вычитания при этом заменяется операцией сложения в ОК или ДК; д) порядок результата берется равным большему порядку; е) если мантисса результата окажется не нормализованной, то производится ее нормализация и коррекция значений порядков. Умножение (деление) требуют различных действий для порядков и мантисс. Алгоритм этих операций выполняется следующим образом: 1)при умножении (делении) порядки ЧПТ складываются (вычитаются); 2)мантиссы ЧПТ перемножаются (делятся); 4)знак произведения (частного) формируется путем сложения знаковых разрядов сомножителей (делимого или делителя). Возможные переносы из знаков разряда игнорируются.

(1)Булева алгебра (алгебра логики) и ее применение при анализе работы ЭВМ. Понятие о булевых (переключательных) функциях (ППФ)

Теоретической основой построения ЭВМ служит специальные математические дисциплины, одной из которых является алгебра логики (булева алгебра). Аппарат булевой алгебры широко используется для описания схем ЭВМ и ЦВМ, а так же для их проектирования и оптимизации. Информация в ЭВМ и цифровых устройствах, так или иначе сводится к ее представлению в 2 СС. На основании зависимости выходных сигналов от входных y=f(x) можно описать любое устройство ЭВМ. Такой зависимостью является булевой функцией, у которой число ее возможных состояний и состояний каждого независимого элемента равно двум (либо 0, либо 1). В технической литературе булевые функции называются логическими или переключательными. Булува алгебра оперирует логическими переменными. Логические переменные может принимать одно из двух значений, да или нет (0;1).

(2)Основные логические операции алгебра логики

На множестве {0;1}  в булевой алгебре определены 3 основных логических операций: а)И (логическое умножение, конъюнкция) . б)НЕ (логическое отрицание, инверсия) . в)ИЛИ (логическое сложение, дизъюнкция) . Каждой из указанных операций может быть задана с помощью табличного соответствия (таблицей истинности). В такой таблице устанавливается взаимнооднозначное соответствие между значениями логических элементов и результатом операций.

переменные		НЕ		И	ИЛИ
Х1	Х2
0	0	1	1	0*0=0
0	1	1	0	0*1=0
1	0	0	1	1*0=0
1	1	0	0	1*1=1

(3)Область определения ПФ, наборы аргументов ПФ, их виды

В общем случае всякая логическая функция имеет свою область определения, охватывающую совокупность комбинаций ее аргументов. Каждая возможная совокупность комбинаций аргументов называется набором. Т.к. любая переключательная функция может принимать только 2 значения, то при наличии n переменных существует 2ⁿ различных наборов аргументов. Число булевых функций будет равно N=2²ⁿ. n=0  N=2; n=1  N=4; n=2  N=16; n=3  N=256; n=4  N=65536. если не известно какие значения принимает булева функция на всех наборах, то она называется неопределенной (частично определенной), а комбинации (наборы), на которые функция неопределенна называется запрещенными. Значения функций на запрещенных наборах можно задать (доопределить) желаемым образом.

(4)Булевы функции двух аргументов и их характеристика

Т.к. результат любой из логической операции принимает значение из того же множества {0;1}, что и аргументы, то можно составить комбинации логических операций, когда результат одной операции используется в качестве операнда в других операциях. Тогда любая логиче5ская операция может быть записана как элементарная логическая функция.

(5)Основные законы алгебры логики

1.Закон одинарных элементов:

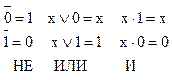
2)законы отрицания (противоречия)

   

3)закон двойного отрицания

4)комбинационные законы

а)тавтология (повторения)

х*х=х

б)коммутативный (переместительный)

х₁*х₂=х₂*х₁

в)ассоциативный (сочетательный)

(х₁*х₂)х₃=х₁(х₂*х₃)

г)дистрибутивный (распределительный)

д)поглощение

 (х₁ поглощает х₂)

е)склеивание

ж)обобщенного склеивания

5)законы дуальности (инверсии, двойственности) (теоремы де Моргана)

6)обобщенные законы дуальности (т.К.Шеннона)

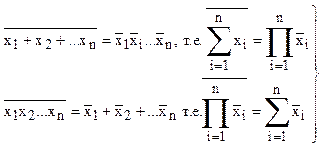
(6)Понятие функциональной полноты системы БФ, основной функционально-полный набор и его смысл

Система булевых функций называется полной, если на ее основе можно получить любую логическую функцию, используя лишь операции суперпозиции. Алгебра логики дает несколько наборов булевых функций, обладающих функциональной полнотой и образующих полный базис простейших функций, из которых могут быть построены сколь угодно сложные функции. В качестве такого набора служит набор из трех булевых функций, носящих название основная функция полного набора. [1] 1)F1(X1,Х2)=(Х1Х2) – конъюнкция, F7(Х1,Х2)=()-дизъюнкция, F12(Х1,Х2)=-инверсия. В общем случае одна из этих функций (F1 или F12) являются излишней, т.к. ее исключение не приводит к нарушению функциональной полноты. [2] 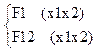[3] 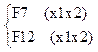. Наборы [2] или [3] отсутствующей по одной операции (функции): ; . Однако работа с переключательными функциями в этих базисах требует от специалистов специальных навыков. При вычислении переключательных функций необходимо соблюдать правила о приоритетах логической операций, которые выполняются в следующем порядке: НЕ, И, ИЛИ. При записывании логических функций для изменения порядка логических операций используют круглые скобки.

(7)Способы задания переключательных функций