Дифференциальное сопротивление RДИФ выпрямительного диода в двух рабочих точках, страница 13

3.1.5 Запись системы контурных уравнений для расчета контурных токов в общем виде

Составим систему контурных уравнений для контурных токов в общем виде

,

,

, где  - комплексные контурные токи;

комплексные ЭДС;

собственные комплексные сопротивления контуров;

взаимные комплексные сопротивления контуров.    

Здесь ,

,

,

,

,

.

3.1.6 Расчет сопротивлений элементов схемы на указанной частоте

,

,

,

,

.

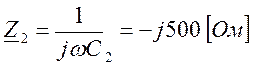3.1.7 Расчет собственных и взаимных сопротивлений

Z ₁₁ = 500 + j300 [Ом],

Z ₁₂ = j300 [Ом],

Z ₂₂ = 200 – j200 [Ом],

Z ₂₃ = 200 [Ом],

Z ₃₃ = 200  + j300 [Ом].

3.1.8 Расчет контурных токов

Систему уравнений будем решать методом Крамера. Найдем сначала определитель системы

.

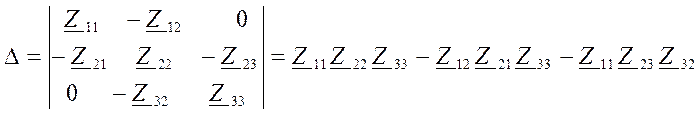Подставляя значения, получим

Определитель для тока

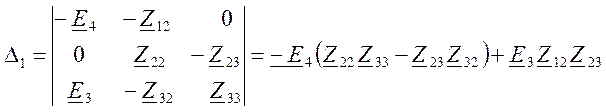
После подстановки значений имеем

.

Разделив  на , получим значение контурного тока

.

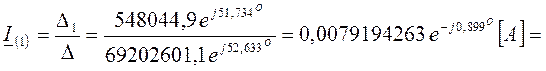
Определитель для тока

.

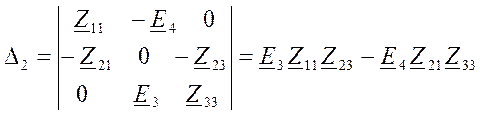Для заданных значений имеем

.

Определим ток контурный ток

.

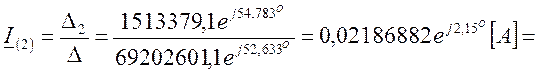
Определитель для тока

.

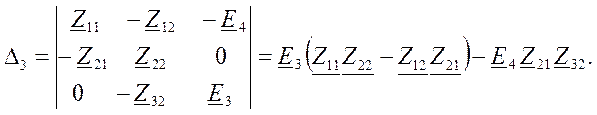Подставляя значения, получим

.

Отсюда контурный ток  равен

.

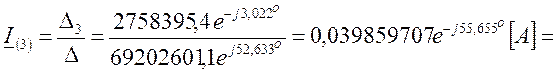
3.1.9 Расчет токов в ветвях и напряжений на элементах.

В соответствии с обозначениями рисунка 3 получаем

.

,

,

,

.

,

,

.

,

.

3.1.10 Проверка правильности решения задачи на основе выполнения законов Кирхгофа

Проверим выполнение 1 закона Кирхгофа.

Для узла А:

.

Для узла В:

.

Следовательно, первый закон Кирхгофа выполняется.

Проверим выполнение 2 закона Кирхгофа.

Для контура 1:

.

Для контура 2:

.

Для контура 3:

.

Таким образом, можно утверждать, что задача решена верно, поскольку законы Кирхгофа выполняются.

3.1.11 Запись результатов в виде мгновенных значений

,

,

,

,

,

,

,

,

,

     .

3.2 Расчет цепи методом узловых напряжений

Пункты 3.2.1 … 3.2.3 полностью совпадают с пунктами 3.1.1 … 3.1.3 соответственно рассмотренного выше алгоритма. Поэтому нумерацию пунктов данного алгоритма начнем с п. 3.2.4.

3.2.4 Обозначение узловых напряжений

Обозначим узлы, например, так, как указано на рисунке 3. В качестве опорного выберем узел , памятуя о том, что таковым может быть любой узел. Напряжения узлов  и  относительно опорного обозначим  и  соответственно.

3.2.5 Запись исходной системы узловых уравнений в общем виде

,

, где      - собственная проводимость узла А;

 - взаимная проводимость узлов А и В;

 - собственная проводимость узла В.

3.2.6 Расчет проводимостей

,

,

,

,

,

,

,

.

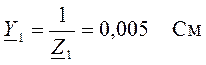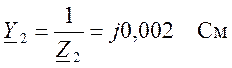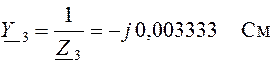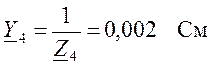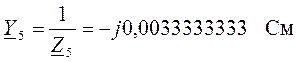3.2.7 Расчет узловых напряжений

Так же, как и в предыдущем случае используем метод Крамера.

Определитель системы равен

.

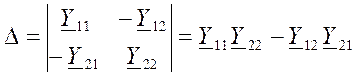Подставляя значения, получим

.

Определитель для напряжения

.

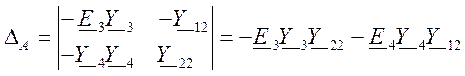После подстановки значений имеем

Следовательно, узловое напряжение  равно

.

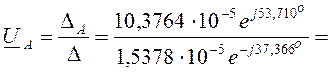
Определитель для напряжения

.

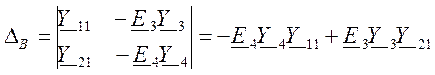После подстановки значений имеем

.

Следовательно, узловое напряжение  равно

.

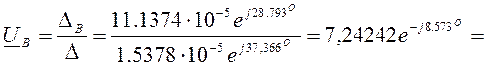
Поскольку  и , что соответствует обозначениям рисунка 3 и решению по методу контурных токов (п.4.19), то в данном примере ограничимся нахождением узловых напряжений и не будем рассчитывать остальные величины.

ЛИТЕРАТУРА

1. Попов В.П. Основы теории цепей: Учебник для вузов / В.П. Попов – 6-е изд., испр. - М.: Высш. шк., 2007. -675 с.

2. Бакалов В.П., Журавлева О.Б., Крук Б.И. Основы анализа цепей: Учебное пособие для вузов / В.П. Бакалов – М.: Горячая линия – Телеком, Радио и связь, 2007. – 591 с.

3. Бессонов Л.А. Теоретические основы электротехники. Электрические цепи: Учебник. – 11-е изд. – М.: Гардарики, 2005. – 638 с.

4. Запасный А.И. Основы теории цепей: Учебное пособие. - М.: РИОР, 2006. – 336 с.

5. Арсеньев Г.Н., Градов И.И. Основы теории цепей: практикум: Учебное пособие / Под ред. Г.Н. Арсеньева – М.: ИД «ФОРУМ»: ИНФРА-М, 2007. – 336 с.

6. Семенцов В.И. Сборник задач по теории цепей: Учебное пособие / В.И. Семенцов, В.П. Попов, В.Н. Бирюков / Под ред. В.П. Попова. – 3-е изд., перераб. и доп. – М.: Высш. шк., 2009. – 270 с.

7. Основы теории цепей. Тестовое оценивание учебных достижений и качества подготовки: Учебное пособие / Под ред. профессора Ю.Ф. Урядникова. – М.: Горячая линия - Телеком, 2007. – 228 с.