Дифференциальное сопротивление RДИФ выпрямительного диода в двух рабочих точках, страница 12

Для т.С: Uсис = 15В; Icc = 11мА;Uзис = 1В                            (5.22)

Для ИРТ: Uсио = 10В; Icо = 10мА;Uзио = 1В

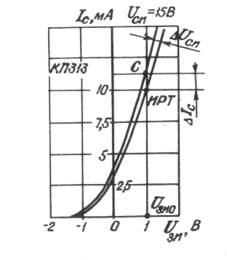Рис.5.12

Для этих двух точек выполняется условие Uзи = 1В = const. По графикам (см. рис.5.12) находим приращения ∆Ic и ∆Uси и определяем параметр Ri

R_i=ΔU_СИ /ΔI_С│_{при Uзи=сonst} =(Uсис-Uсио)∕(Icc-Icо)=(15В-10В)∕(11мА-10мА)=5кОм        (5.14)

Определение коэффициента усиления μ

Для определения коэффициента усиления μ в соответствии с формулой (5,7) для выполнения условия Ic = const выберем на характеристике Ucи = 15 В точку т.Д, для которой Ic = 10 мА (рис. 5,13)

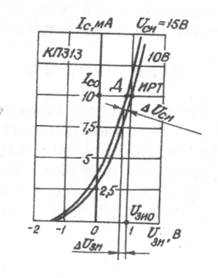Рис. 5.13

Для т.Д: Uсид = 15В; Uзид = 0,85В; Iсд = 10мА                         (5.24)

Для ИРТ: Uсио = 10В; Uзид = 1В; Iсо = 10мА

Для этих двух точек выполняется условие Iс = 10мА=const.

По графикам (см.рис.5.13) находим приращения ∆Uзи и ∆Ucи и определяем коэффициент усиления μ..

μ=│∆Ucи∕∆Uзи│_{приIс=10мА=const}=(Uсид–Uсио)∕(Iсд-Iсо)=(15В-10В)∕(1В-0,85В)=38,5      (5.25)

Расчет по формуле  (5.8)

μ = SRi = 8,3 мА 5кОм = 41,5                                         (5.26)

дает удовлетворительное согласование с (5.25). Небольшие расхождения обусловлены неизбежными погрешностями графических построений и не играют существенной роли. Как уже отмечалось выше, существует разброс параметров у транзисторов.

Таблица 4 – Данные варианта задания 4 на курсовую работу.

Рисунок 1 – Обобщенная схема электрической цепи

Значения элементов ветвей приведены в таблице 1.

Таблица 1 - Значения элементов ветвей электрической цепи

Ветвь 1	Ветвь 2	Ветвь 3	Ветвь 4	Ветвь 5
R, Ом	C, нФ	L, МГн	R, Ом	L, мГн
200	200	30	500	30

В таблице 2 приведен номер варианта и  задания на курсовую работу.

Таблица 2 – Вариант задания на курсовую работу.

Номер варианта	Ветвь 1	Ветвь 2	Ветвь 3	Ветвь 4	Ветвь 5
65	R	C	L	R	L

 

2 СОДЕРЖАНИЕ КУРСОВОЙ РАБОТЫ

Курсовая работа предусматривает решение одной задачи, в которой   необходимо:

- изобразить расчетную и комплексную схемы замещения электрической цепи, обозначив входящие в нее элементы;

- рассчитать методом контурных токов и узловых напряжений токи в ветвях и падения напряжений на элементах цепи;

- записать их аналитические выражения для мгновенных значений;

- проверить выполнение 1 и 2 законов Кирхгофа.

3.1 Расчет методом контурных токов

3.1.1 Изображение расчётной схемы замещения электрической цепи.

Пусть в первой и четвертой ветвях содержатся сопротивления, в третьей и пятой – индуктивности, а во второй – емкость.

Тогда расчетная схема замещения цепи будет иметь вид, изображенный на рисунке 2.

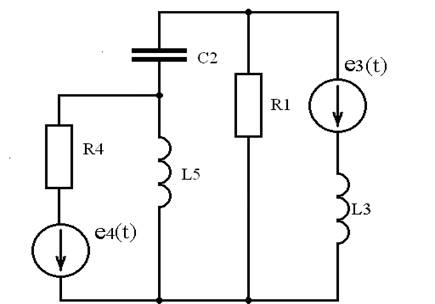
Рисунок 2 - Расчётная схема замещения электрической цепи

3.1.2 Изображение комплексной схемы замещения

Комплексная схема замещения цепи изображена на рисунке 3.

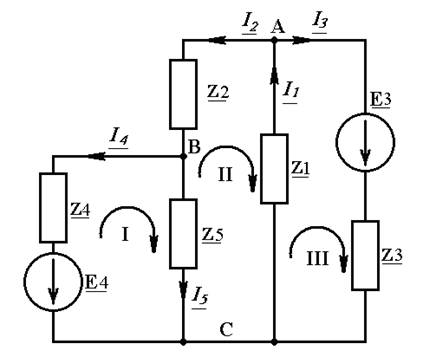
Рисунок 3 – Комплексная схема замещения электрической цепи

Цепь имеет 3 узла (A,B,C) и 5 ветвей. Следовательно, при использовании метода уравнений Кирхгофа необходимо решать систему из 7 уравнений.

Метод контурных токов позволяет решать систему из 3 уравнений, так как в цепи 3 независимых контура.

3.1.3 Выбор положительных направлений токов в ветвях

Условные положительные направления токов в ветвях выбираются произвольно. Выберем их так, как указано на рисунке 3.

3.1.4 Выбор направления обхода и обозначение независимых контуров

Контурные токи обозначим также произвольно, например, по часовой стрелке, как на рисунке 3. Положительные направления обхода контуров выберем совпадающим с направлениями контурных токов.