Принятие решения в организационно-управленческих задачах, страница 3

Подсчитаем суммарную коммуникабельность, которое показали работники при выполнении указанных операций:

C₂= x₁₁*8+x₁₂*8+ x₁₃*8+…+ x₁₅*8+ x₂₁*7+ x₂₂*7+…+ x₂₅*7+ x₃₁7+ x₃₂*7+…+ x₃₅*7+ x₄₁*5+ x₄₂*5+………….+ x₉₄*7+ x₉₅*7.

Подсчитаем суммарное требование к оплате:

C₃= x₁₁*26+x₁₂*24+ x₁₃*25+…+ x₁₅*26+ x₂₁*12+ x₂₂*17+…+ x₂₅*28+ x₃₁*11+ x₃₂*14+…+ x₃₅*27+ x₄₁*15+ x₄₂*18+………….+ x₉₄*16+ x₉₅*27.

В каждой строке табл. 1 может находится не более одного назначения. Поэтому сумма переменных x_ij для каждой i-й стоки также должна быть равна 1 или 0:

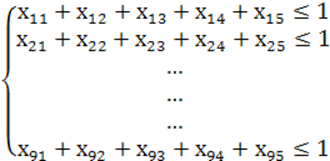                  (1.1)

Каждую операцию обязательно нужно выполнить, но назначить н нее более одного рабочего места нельзя. Следовательно, каждый столбец будет содержать только одну единицу и остальные нули. Поэтому сумма x_ij для каждого j-ого столбца в таблице 2 должна быть равна 1, следовательно:

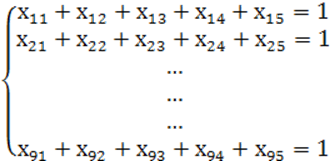     (1.2)

Кроме того, все искомые переменные неотрицательны:

x_ij0, где i=1, 2, …, 9; j=1, 2, …,5.   (1.3)

Также следует учесть информацию о том, что Репин является дальним родственником, а Костин обладает вздорным характером. Из этого следует то, что у Репина больше шансов устроиться, а Костина нужно исключить из списка кандидатов как скандалиста.

Для решения задач распределенного типа, к числу которых относится и рассматриваемая, целесообразно использовать транспортные алгоритмы. Поиск решения в Excel автоматически «распознает» такие задачи и использует для решения соответствующие вычислительные алгоритмы, которые значительно более эффективны, чем, например, симплекс-метод. Это обстоятельство играет важную роль, особенно для задач большой размерности.

Ход решения задачи в Excel рассматривается ниже на рисунках и табли-цах. На рисунке 1 показана модель переменных с ограничениями.  Т.е. в столбце N  и строке 15 мы организовали ограничение на общее условие задачи, а в ячейках, К16, – на дополнительные.

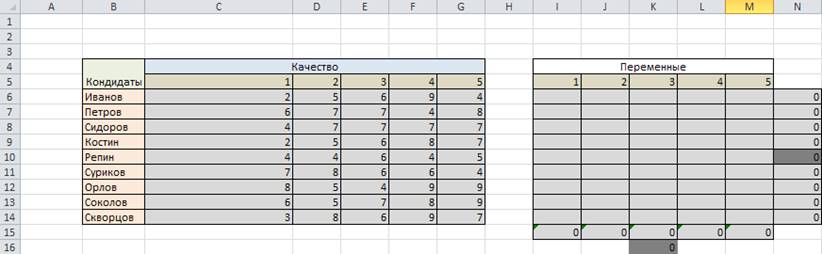
Рис.1  Табличное представление модели в Excel с ограничениями на  X_ij

В таблице 3 представлены формулы нахождения целевых функций.

Таблица 3

Нахождение целевых функций

Для анализа зависимости критериев друг от друга построим область изменений их значений как показано на рисунке 2. Проанализируем зависимость суммарной производительности и показателя качества от фонда заработной платы (Таблица 4).

 Таблица 4

Качество	38	40	34	34	34	39	38	36
Оплата	120	115	110	105	100	95	90	85
Производит	101	87	100	94	91	94	89	88

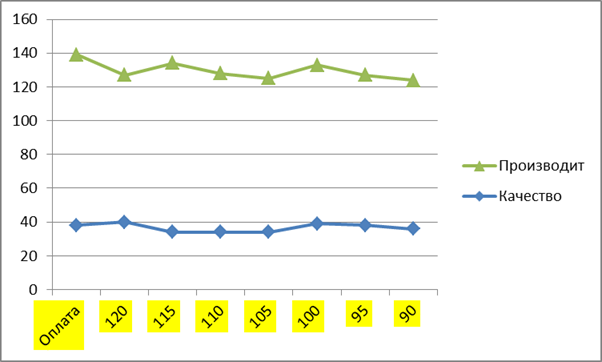
Рис. 2 Зависимости критериев.

Из графика видно, что три критерия уже не отражают оптимальную зависимость друг перед другом. Т. е. определить, сколько минимально возможно выделить денег на оплату труда, чтобы получить максимально-оптимальные значения по качеству и производительности, становится сложно.

Поэтому перейдем к разработке прямой ЧМП, по итогам которой мы должны найти глобальное решение нашей задачи. Но перед дальнейшим решением

Из графика видно, что три критерия уже не отражают оптимальную зависимость друг перед другом. Т. е. определить, сколько минимально возможно выделить денег на оплату труда, чтобы получить максимально-оптимальные значения по качеству и производительности, становится сложно.

Поэтому перейдем к разработке прямой ЧМП, по итогам которой мы должны найти глобальное решение нашей задачи. Но перед дальнейшим решением произведем нормирование  критериев по формуле на рисунке 3, определив диапазон  изменения от 0 до 1:

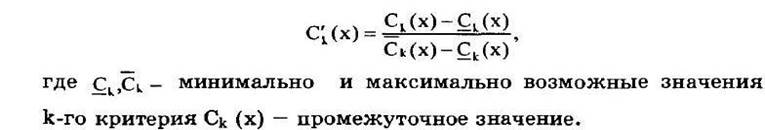
Рис 3 Нормирование критериев.