
Дифференцирование изображений
Рассмотрим теорему о
дифференцировании изображения ![]() по аргументу q.
по аргументу q.
Теорема 8. Если ![]() является оригиналом, а
является оригиналом, а ![]() - ее изображением, то справедливо
равенство:
- ее изображением, то справедливо
равенство:
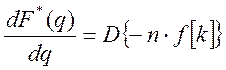 (1)
(1)
Доказательство:
Дифференцируя ряд 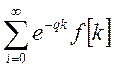 по аргументу q,
получаем:
по аргументу q,
получаем:
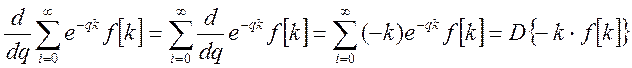
Мы поменяли порядок суммирования
и дифференцирования. Почленное дифференцирование ряда 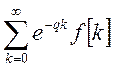 возможно,
если ряд, состоящий из производных, сходится равномерно.
возможно,
если ряд, состоящий из производных, сходится равномерно.
Для того, чтобы в этом убедиться, определим абсциссу абсолютной сходимости в уравнении (1). Так как ряд
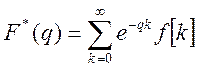
сходится абсолютно в каждой
точке, где ![]() и расходится, где
и расходится, где ![]() .
.
Здесь справедливо следующее:
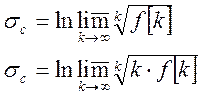
Рассмотрим предел под знаком логарифма:
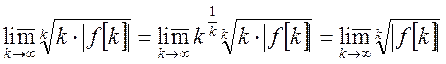
Это значит, что абсцисса
абсолютной сходимости ряда 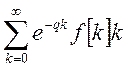 совпадает с абсциссой
абсолютной сходимости ряда
совпадает с абсциссой
абсолютной сходимости ряда 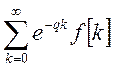 . И поэтому ряд
. И поэтому ряд 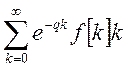 сходится абсолютно, где выполняется
неравенство
сходится абсолютно, где выполняется
неравенство ![]() . Таким образом почленное
дифференцирование ряда
. Таким образом почленное
дифференцирование ряда 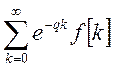 допустимо
справедлива общая формула дифференцирования изображения:
допустимо
справедлива общая формула дифференцирования изображения:
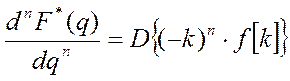
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.