Анализ устойчивости цифровой системы

4.4. Анализ устойчивости цифровой системы.

Устойчивость замкнутой цифровой системы определяется видом корней характеристического уравнения. На s-плоскости корни устойчивой системы должны лежать в левой полуплоскости. Переход к комплексной переменной z=e^sT отображает левую полуплоскость во внутреннюю часть круга единичного радиуса с центром в начале координат z-плоскости (см. рис. 1). Поэтому в устойчивой системе корни характеристического уравнения (знаменателя передаточной функции замкнутой системы, приравненного нулю)

1 + W (z) = 0                                                             (1)

должны лежать внутри круга единичного радиуса, т. е. быть по модулю меньше единицы |zJ<l. Здесь i = l, 2, ..., k, где k— порядок знаменателя передаточной функции замкнутой системы.

4.4.1. Алгебраические критерии устойчивости.

Итак, цифровая система устойчива, если корни характеристического уравнения системы лежат внутри единичного круга на z-плоскости. Однако нахождение корней характеристического уравнения высокого порядка представляет обычно очень сложную задачу. Поэтому для определения факта устойчивости или неустойчивости системы применяют различные критерии устойчивости.

Критерий Шура-Кона

Проверка расположения нулей полинома F(z) внутри или вне единичного круга может быть выполнена с помощью алгебраического критерия Шура-Кона. Рассмотрим методику применения этого критерия.

Пусть имеется полином (характеристический полином замкнутой системы)

F(z) = a₀ + a₁z + a₂z² +… + a_nzⁿ                                                                  (2)                  

Если все определители                                                                                          

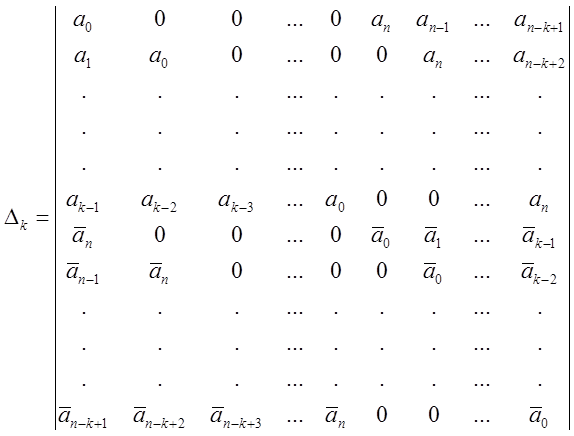                                    (3)

где k = 1, 2, ..., п и ā_k - величина, сопряженная с а_k, отличны от нуля, то F (z) не имеет нулей на окружности единичного радиуса |z| = l и число нулей внутри этого круга Р равно числу перемен знака в последовательности определителей.

Для того чтобы импульсная система была устойчивой, все корни характеристического уравнения должны лежать внутри круга единичного радиуса. Это означает, что число перемен знака в последовательности определителей 1, Δ₁, Δ₂, …,Δ_n  должно быть равно п, где п—степень характеристического уравнения.

Итак, критерий устойчивости может быть сформулирован следующим образом:

Δ_k < 0, если k нечетное,

Δ_k  > 0, если k четное.                                                                                 (4)

Например, в случае полинома второй степени n = 2 для последовательности           1, Δ₁, Δ₂  должны выполняться следующие неравенства:

 Δ₁ < 0,  Δ₂ > 0,

Указывающие на то, что для того, чтобы два корня характеристического уравнения лежали внутри единичного круга, необходимы две перемены знака. В этом примере  Δ₁ и Δ₂ соответственно равны:

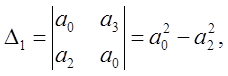
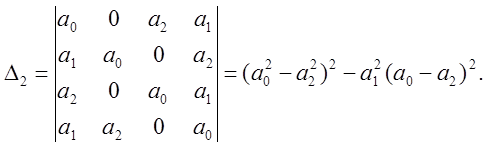
Условия устойчивости могут быть выражены через коэффициенты характеристического уравнения

a₀ + a₁z + a₂z²

следующим образом:

           

Для систем более высокого порядка аналогичным образом могут быть получены соотношения, требующие вычисления определителей более высокого порядка. Однако существует более практичный метод проверки устойчивости, который позволяет избежать вычисления определителей высокого порядка.

Применение критерия Гурвица

Критерий Гурвица позволяет определить находятся или нет все корни полинома комплексной переменной в левой комплексной полуплоскости. Таким образом, если выполнить комфорное преобразование единичного круга в z-плоскости на левую полуплоскость другого комплексного аргумента w, то все корни полинома F(z), лежащие внутри единичного круга перейдут на левую полуплоскость аргумента w, а корни полинома F(z), лежащие вне единичного круга на z-плоскости окажутся на правой полуплоскости аргумента w. Необходимое преобразование, называемой билинейным преобразованием или w-преобразованием, выполняется подстановкой

       z = (w + 1            )/(w – 1)                                                                     (5)

Таким образом, порядок применения критерия Гурвица для оценки устойчивости цифровой системы управления может быть следующим. Характеристическое уравнение системы в плоскости z с помощью подстановки (5) преобразуется в уравнение

 b₀wⁿ + b₁w^n-1 + b₂w^n-2 + … + b_n = 0,                                               (6)

из коэффициентов которого составляется матрица Гурвица:

            b₁  b₃   b₅  … 0      0

            b₀  b₂   b₄  … 0      0

0  b₁  b₃  … 0      0

…………………….                                                                          (7)

0    0     0        b_n-1 0

0    0     0        b_n-2 b_n

Система оказывается устойчивой, если при b₀ > 0 положительны n определителей Гурвица, получаемых их (7), т.е.

b₀ > 0; Δ₁ = b₁ > 0;           | b₁  b₃ | 

                                Δ₂ =  | b₀  b₂  |  > 0; … , Δ_n = b_n Δ_n-1 > 0.                      (8)