Анализ устойчивости заданной системы управления методами: Ляпунова, Рауса, Гурвица, Льенера-Шипара, Михайлова, Найквиста, D-разбиения, Шур-Кона

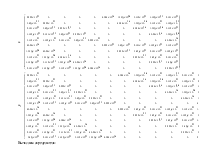
Дано.

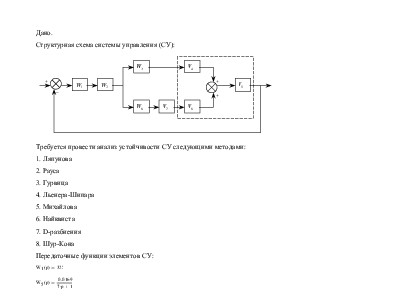
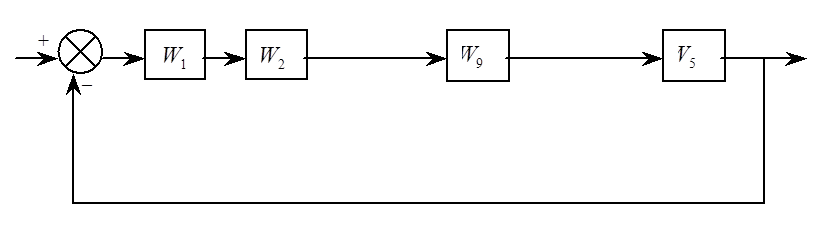
Структурная схема системы управления (СУ):

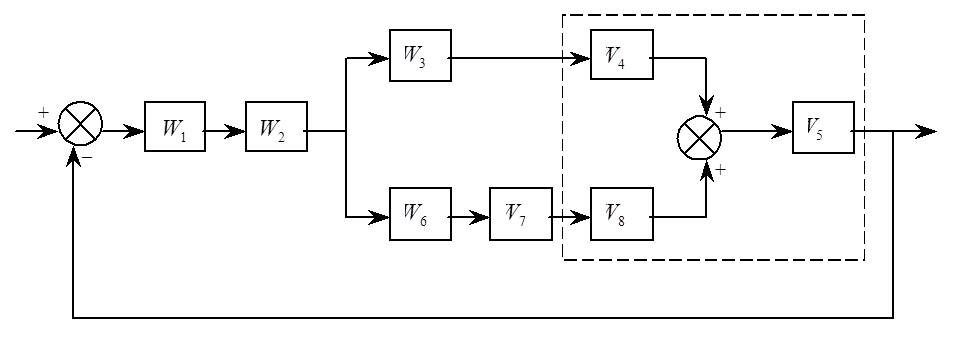
Требуется провести анализ устойчивости СУ следующими методами:

1. Ляпунова

2. Рауса

3. Гурвица

4. Льенера-Шипара

5. Михайлова

6. Найквиста

7. D-разбиения

8. Шур-Кона

Передаточные функции элементов СУ:

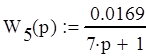
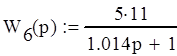
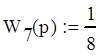
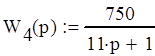
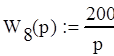
Решение.

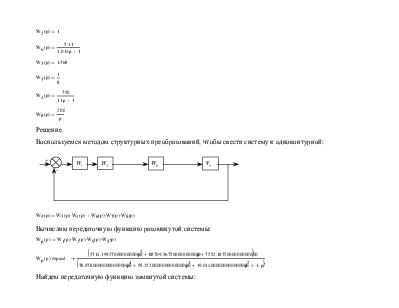
Воспользуемся методом структурных преобразований, чтобы свести систему к одноконтурной:

Вычислим передаточную функцию разомкнутой системы:

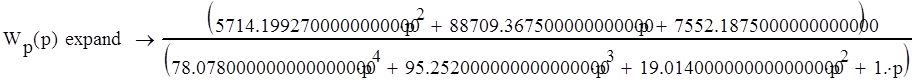
Найдем передаточную функцию замкнутой системы:

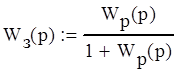
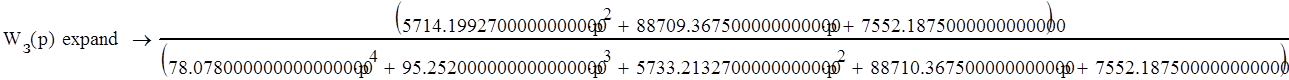
Система удовлетворяет необходимому условию устойчивости, так как все коэффициенты характеристического уравнения, получающегося путем приравнивания знаменателя передаточной функции системы 0, положительны.

Линейная САУ является устойчивой по критерию Ляпунова, если все корни характеристического уравнения лежат в левой полуплоскости, то есть их действительная часть меньше 0.

Составим характеристическое уравнение замкнутой системы:

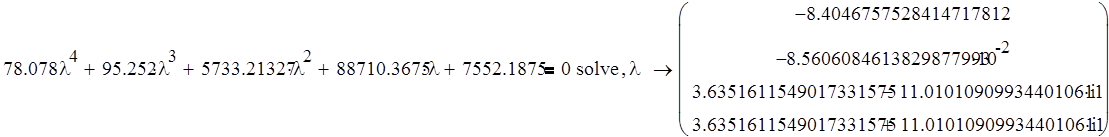
Уравнение имеет 2 действительных корня, лежащих в левой комплексной полуплоскости, и 2 комплексно-сопряженных корня, лежащих в правой комплексной полуплоскости, следовательно система неустойчива.

Определим область устойчивости системы методом D-разбиения.

D-разбиение - разбиение плоскости искомого параметрана области, в которых число корней с положительной действительной частью постоянно. Область устойчивости - область с числом корней с положительной вещественной частью, равным 0. Оптимальное значение параметра выбирается на вещественной оси в середине области устойчивости. Граница D-разбиения - решение характеристического уравнения D(jw) = 0 для искомого параметра при w = -¥ ... +¥.

Построим D-разбиение по параметру k3.

Передаточная функция разомкнутой системы:

Передаточная функция замкнутой системы:

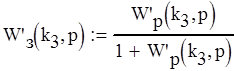
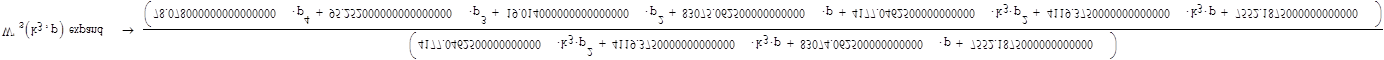
Характеристический полином:

Решим его относительно искомого параметра:

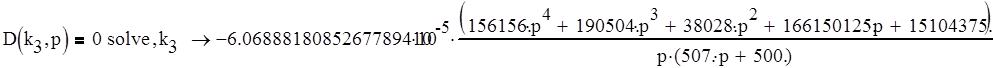
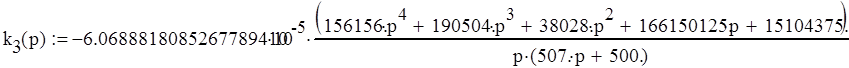
Заменим комплексную переменную p на чисто мнимую jw:

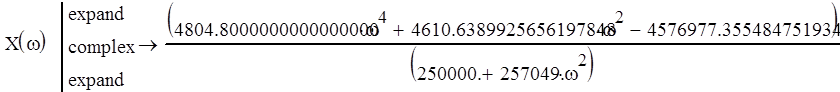
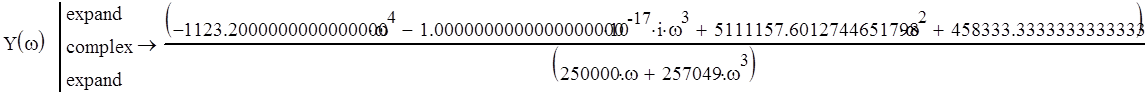
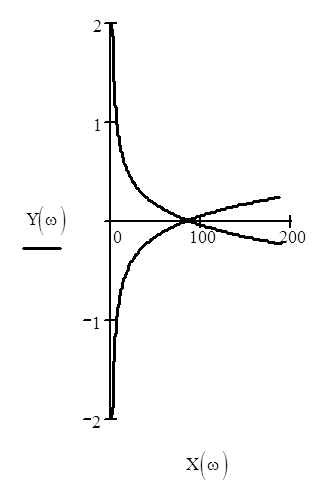
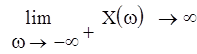
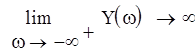
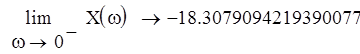
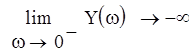
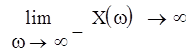
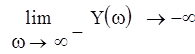
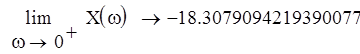
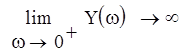
Найдем точку пересечения кривых с осью:

По правилу штриховки штрихуется левая (в направлении возрастания частоты) часть кривой.

При переходе через границу D-разбиения в сторону штриховки, число корней с положительной вещественной частью уменьшается на 1, следовательно в нашем случае областью устойчивости будет область, ограниченная этими кривыми и содержащая положительную вещественную полуось от точки пересечения кривых до бесконечности. Значение параметра выбирается на вещественной положительной полуоси в середине области устойчивости. Так как она не ограничена справа, то возможно любое значение параметра, большее 85.

Примем значение параметра, равным 136.8.

Вычислим передаточную функцию разомкнутой системы:

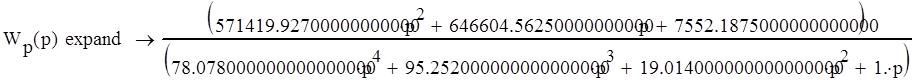
Найдем передаточную функцию замкнутой системы:

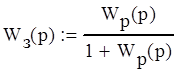
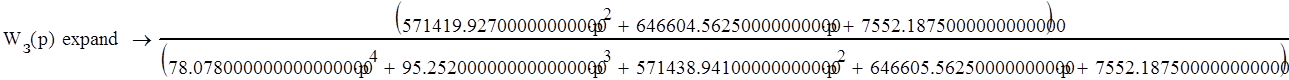
Система удовлетворяет необходимому условию устойчивости, так как все коэффициенты характеристического уравнения, получающегося путем приравнивания знаменателя передаточной функции системы 0, положительны.

Линейная САУ является устойчивой по критерию Ляпунова, если все корни характеристического уравнения лежат в левой полуплоскости, то есть их действительная часть меньше 0.

Составим характеристическое уравнение замкнутой системы:

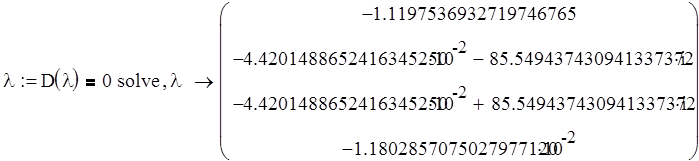
Отметим корни уравнения на комплексной плоскости.

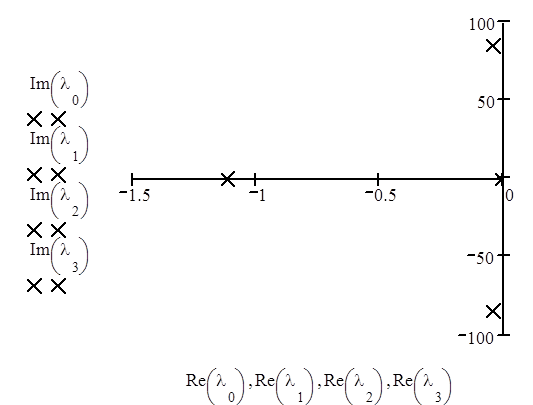
Уравнение имеет 2 действительных отрицательных корня, и 2 комплексно-сопряженных корня, лежащих в левой комплексной полуплоскости, следовательно система является устойчивой, статической, колебательно-апериодической 4 порядка.

Определим устойчивость замкнутой системы по методу Рауса.

Составим программу для построения таблицы Рауса:

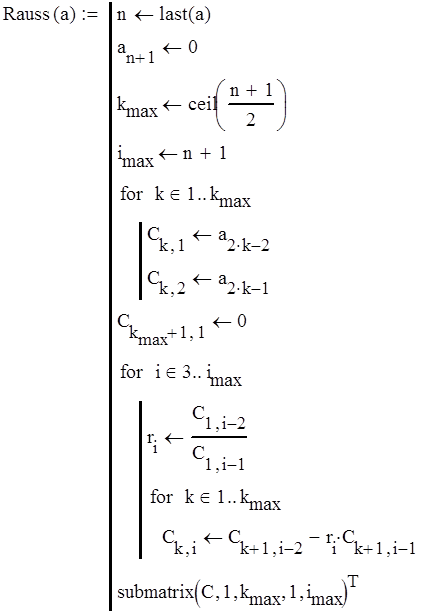
Коэффициенты характеристического уравнения:

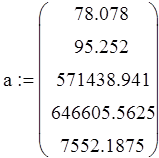
Построим таблицу Рауса:

Поскольку все коэффициенты 1 столбца таблицы положительны, система устойчива.

Определим устойчивость системы по методу Гурвица.

Составим программу для построения определителей Гурвица:

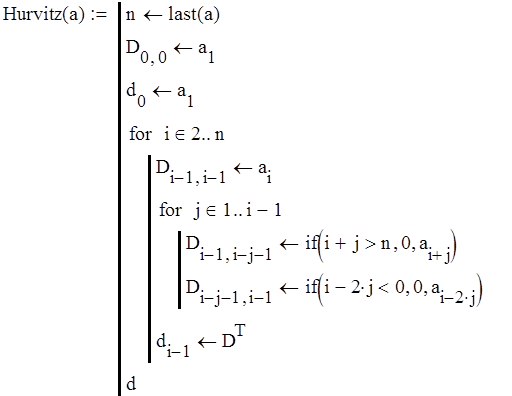
Построим определители Гурвица:

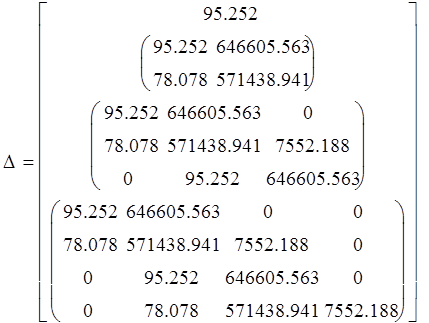
Вычислим определители:

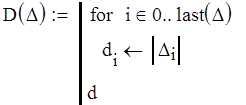
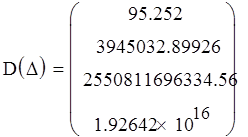
Все определители Гурвица положительны, следовательно система устойчива.

Критерий Льенера-Шипара состоит в следующем: если выполняется необходимое условие устойчивости (все коэффициенты характеристического уравнения положительны), достаточно вычислить только четные (нечетные) определители Гурвица; если все они положительны, система устойчива.

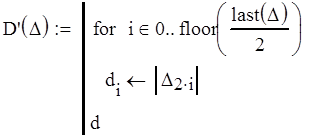
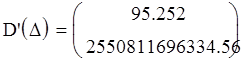
Все нечетные определители Гурвица больше 0, следовательно система устойчива.

Определим устойчивость СУ по критерию Михайлова.

Заменим в характеристическом уравнении p на jw и выделим действительную и мнимую части:

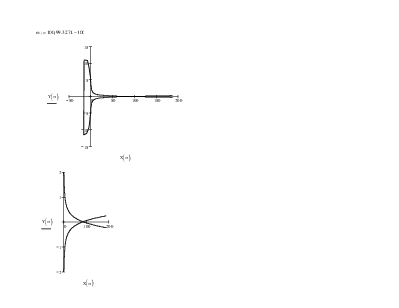
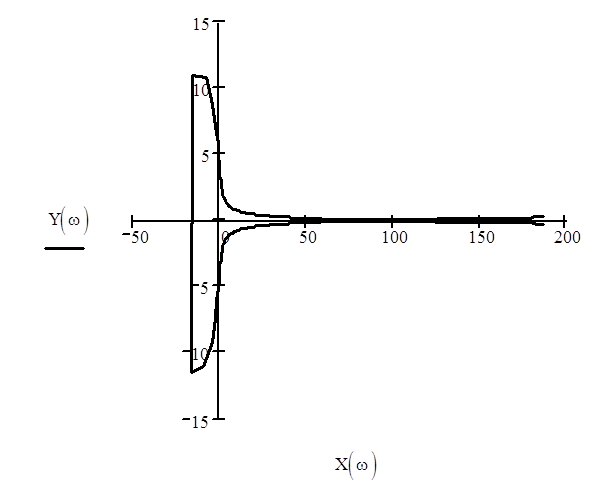
Построим годограф Михайлова:

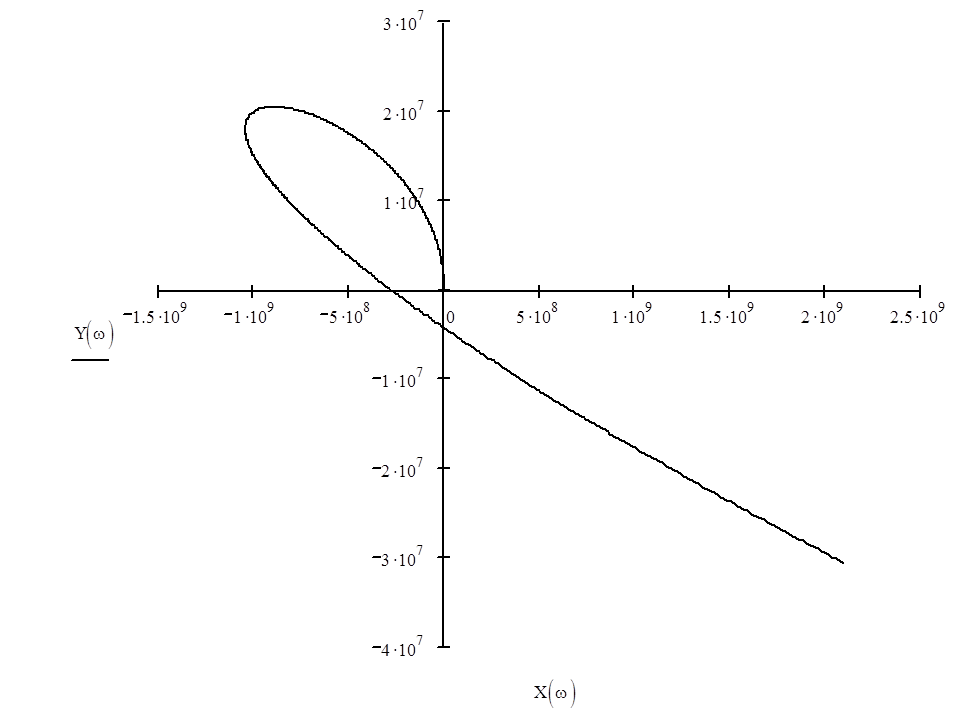
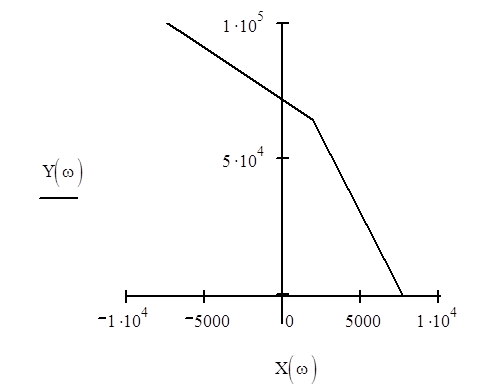
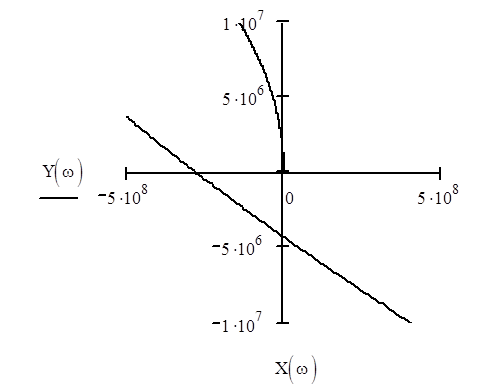
Система устойчива по критерию Михайлова, если годограф Михайлова, начинаясь на положительной вещественной полуоси, при изменении частоты от нуля до бесконечности поворачивается, в соответствии с принципом аргумента, в положительном направлении вокруг начала координат последовательно, нигде не обращаясь в ноль на n квадрантов, где n - порядок характеристического уравнения.

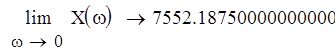
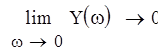
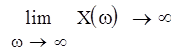
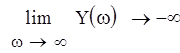
Как видно из графика, кривая Михайлова началась на вещественной положительной полуоси и прошла 4 квадранта в положительном направлении, нигде не обращаясь в 0, следовательно система устойчива.

Определим устойчивость замкнутой САУ по АФЧХ разомкнутой методом Найквиста.

В первую очередь определим устойчивость разомкнутой системы, воспользовавшись критерием Ляпунова:

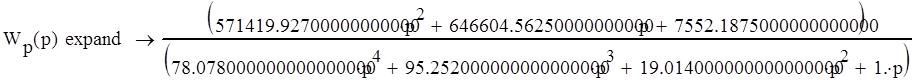
Составим характеристическое уравнение разомкнутой системы, приравняв знаменатель ее передаточной функции нулю, и найдем его корни:

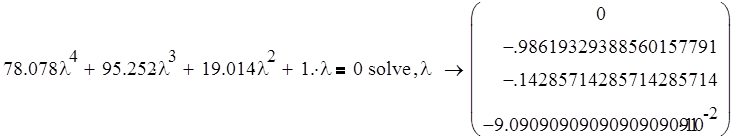
Уравнение имеет 3 действительных отрицательных корня и 1 нулевой корень, следовательно система является устойчивой, астатической 1 порядка.

Найдем АФЧХ разомкнутой системы:

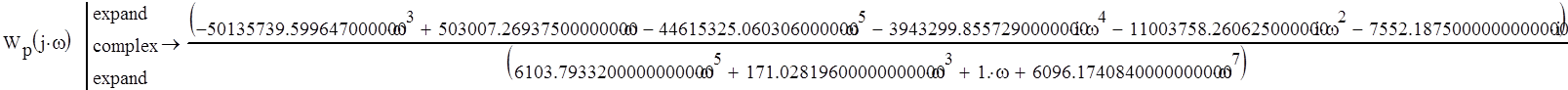
Выделим действительную и мнимую части:

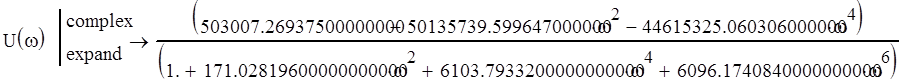
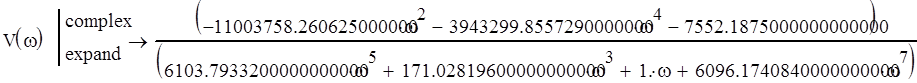
Построим годограф Найквиста (АФЧХ разомкнутой системы):

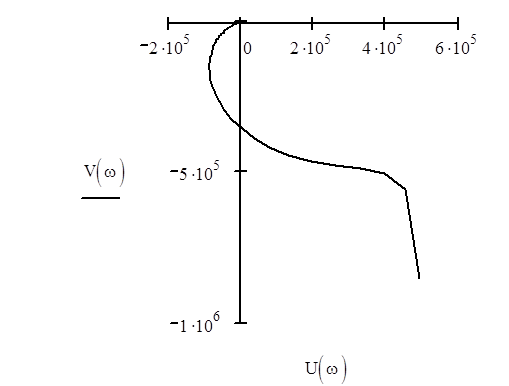
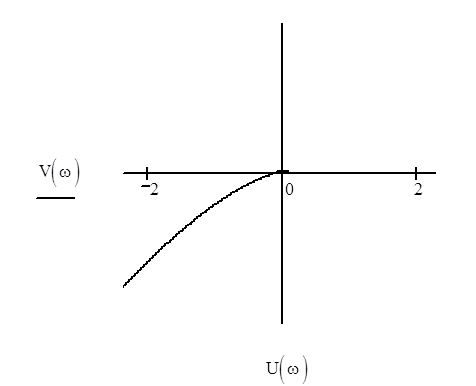
Чтобы САУ, устойчивая в разомкнутом состоянии, была устойчива в замкнутом, необходимо и достаточно, чтобы кривая АФЧХ разомкнутой системы при изменении частоты от нуля до бесконечности не охватывала точку (-1 + j0).

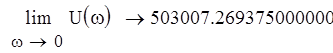
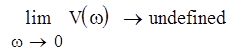
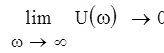
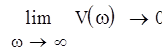
Так как система астатическая 1 порядка, достроим получившийся график дугой бесконечного радиуса, которая поворачивается на угол от 0 до (p/2)*n, где n=1 - порядок астатизма, при w=0. Как видно из графика, годограф Найквиста не охватывает точку (-1 + j0), следовательно система будет устойчива в замкнутом состоянии.

Так как система является дискретной (содержит элемент с передаточной функцией, равной 1), определим ее устойчивость методом Шур-Кона.

Для этого найдем дискретную передаточную функцию системы в форме z-изображения.

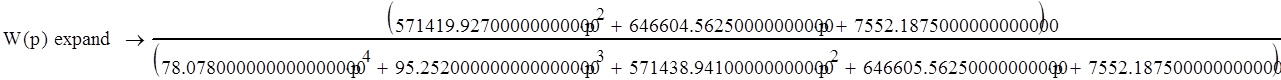
Вычислим непрерывную весовую функцию системы:

Найдем решетчатую весовую функцию.

Зададим период дискретизации:

Заменим непрерывную переменную t дискретными значениями kT0, где k = 0,1,2,... - номер момента времени, а T0 = const - период дискретизации. При t = kT0 значение решетчатой функции равно значению непрерывной функции (огибающей) в тот же момент времени, в остальные моменты значение решетчатой функции равно 0.

Произведем z-преобразование решетчатой весовой функции.

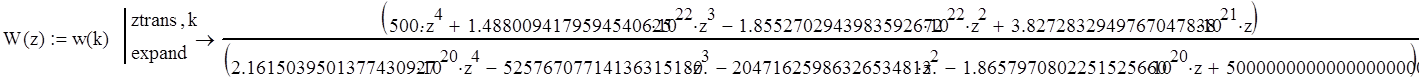
Дискретная передаточная функция системы:

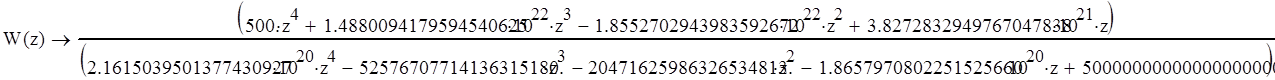
Домножим на фиксатор нулевого порядка:

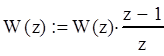
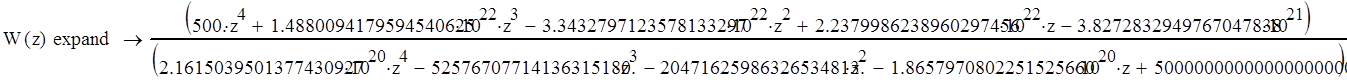
Составим характеристическое уравнение дискретной системы, приравняв знаменатель дискретной передаточной функции нулю:

Переходный процесс в линейной дискретной системе будет сходящимся при условии, что все корни характеристического уравнения по модулю не превышают 1.

Это условие означает, что все корни характеристического уравнения устойчивой замкнутой импульсной системы должны в плоскости z лежать внутри окружности единичного радиуса.

Известно, что билинейное преобразование переводит точки этой окружности на плоскости z в точки, лежащие на мнимой оси плоскости w. При этом область внутри окружности переходит в левую полуплоскость w.

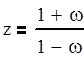
Таким образом, чтобы дискретная система была устойчива, необходимо и достаточно, чтобы все корни преобразованного характеристического уравнения, получившегося из исходного при помощи замены z = (1+w)/(1-w) (w-преобразования), были расположены слева от мнимой оси плоскости w, что можно проверить при помощи критериев устойчивости для непрерывных систем.

Найдем корни характеристического уравнения дискретной системы:

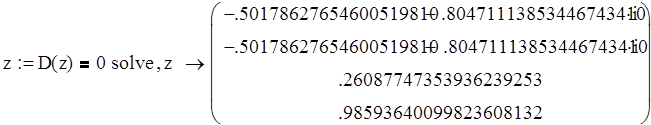
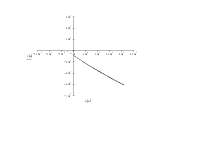
Изобразим корни на комплексной плоскости z:

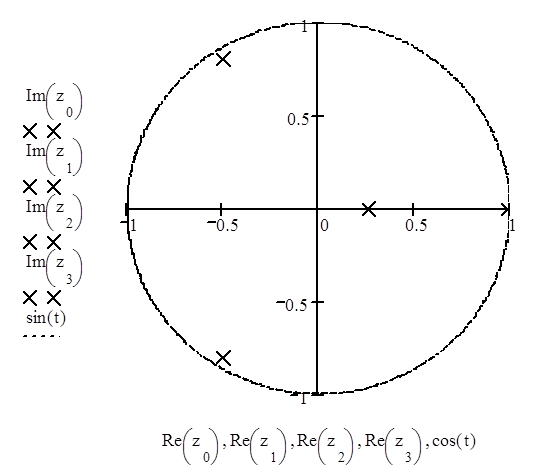
Вычислим их модули:

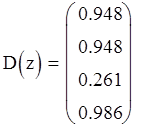
Так как они не превышают 1, то есть лежат внутри единичной окружности на плоскости z, дискретная система является устойчивой.

Произведем билинейное преобразование исходного характеристического уравнения:

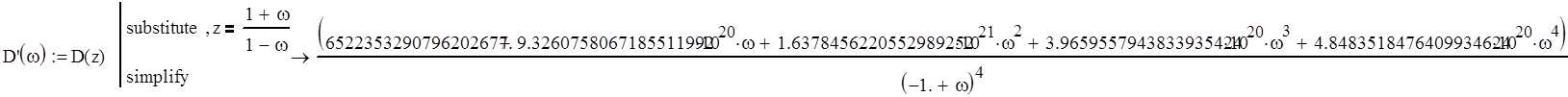
Найдем корни преобразованного характеристического уравнения:

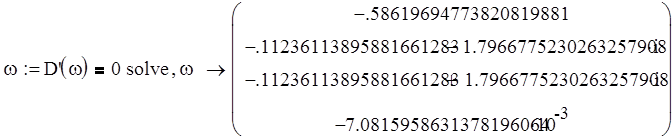
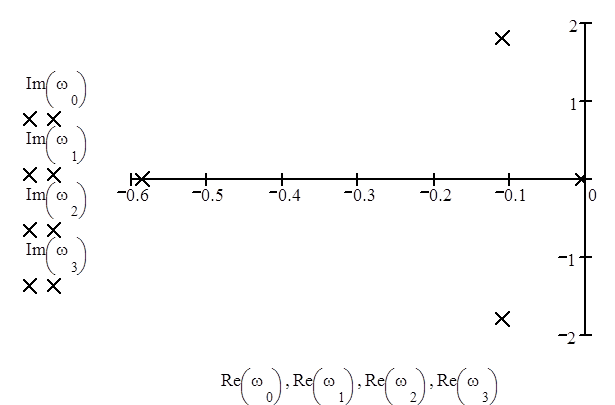
Уравнение имеет 2 действительных отрицательных корня и 2 комплексно-сопряженных корня, лежащих слева от мнимой оси, то есть их действительные части отрицательны, следовательно дискретная система устойчива.

Анализ устойчивости импульсных систем может быть проведен и без w-преобразования, по коэффициентам исходного (непреобразованного) характеристического уравнения. В этом случае используется алгебраический критерий Шур-Кона, согласно которому импульсная система устойчива, если составленные из коэффициентов характеристического уравнения определители нечетных порядков будут меньше 0, а определители четных порядков - больше 0.

Составим определители по Шур-Кону из коэффициентов уравнения.

Составим программу для построения определителей Шур-Кона:

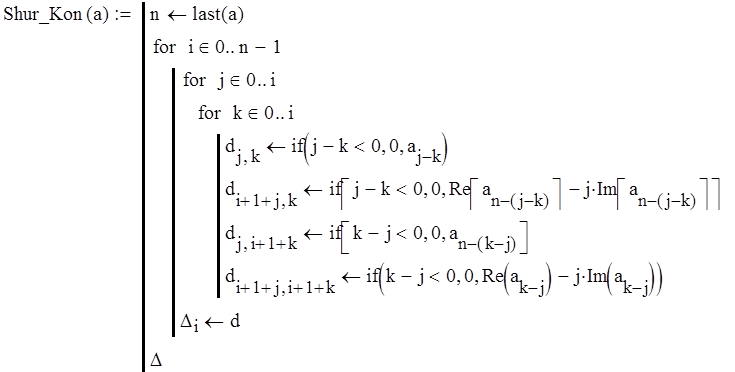
Составим вектор коэффициентов характеристического уравнения:

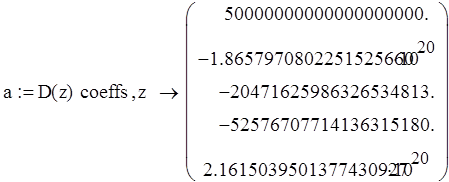
Построим определители:

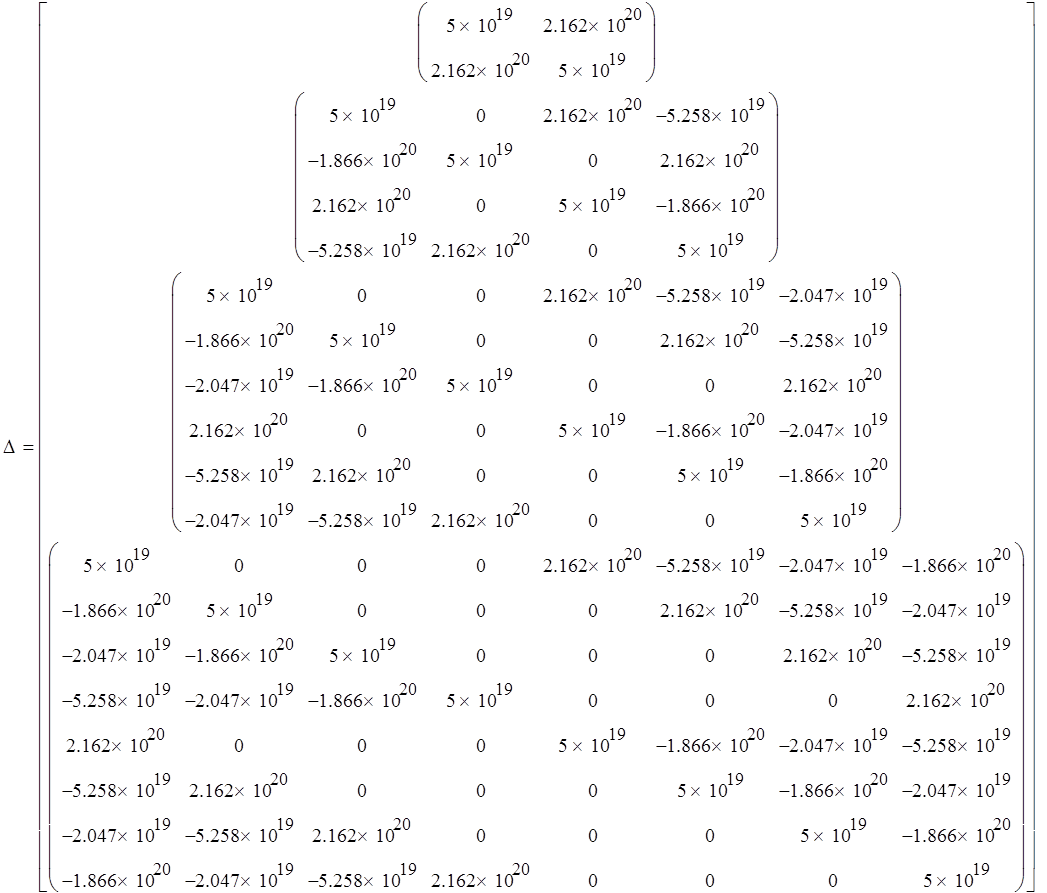
Вычислим определители:

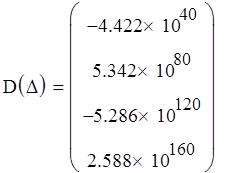
Так как знаки определителей на четных и нечетных местах чередуются, причем нечетные определители меньше нуля, а четные - больше, то дискретная система является устойчивой.

Заменим комплексную переменную z на псевдочастоту:

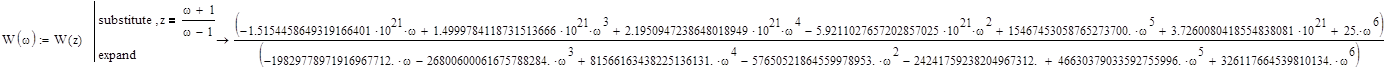
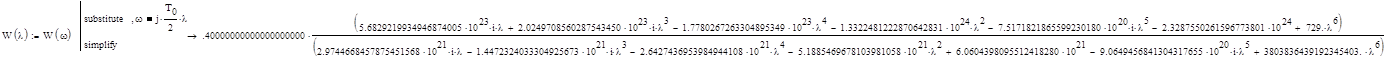
Составим характеристическое уравнение относительно l:

Составим вектор коэффициентов характеристического уравнения:

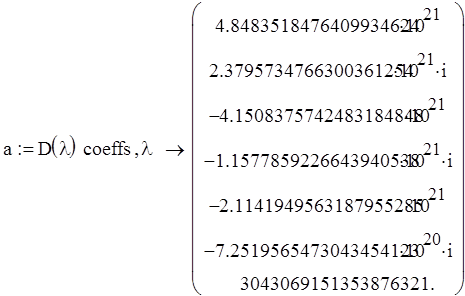
Построим определители:

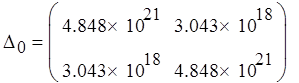
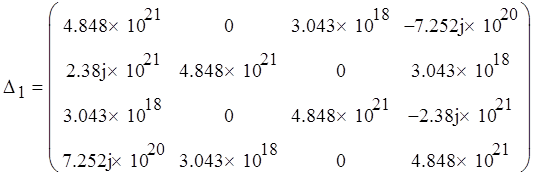
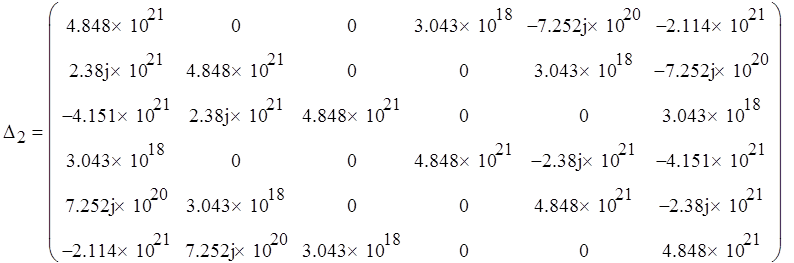
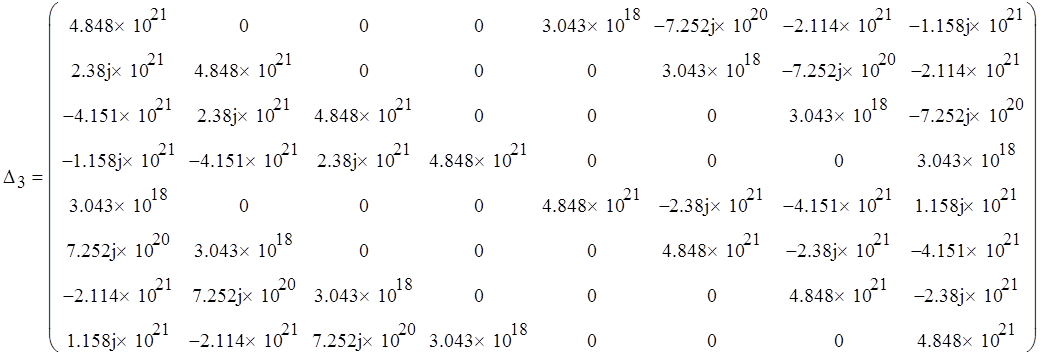
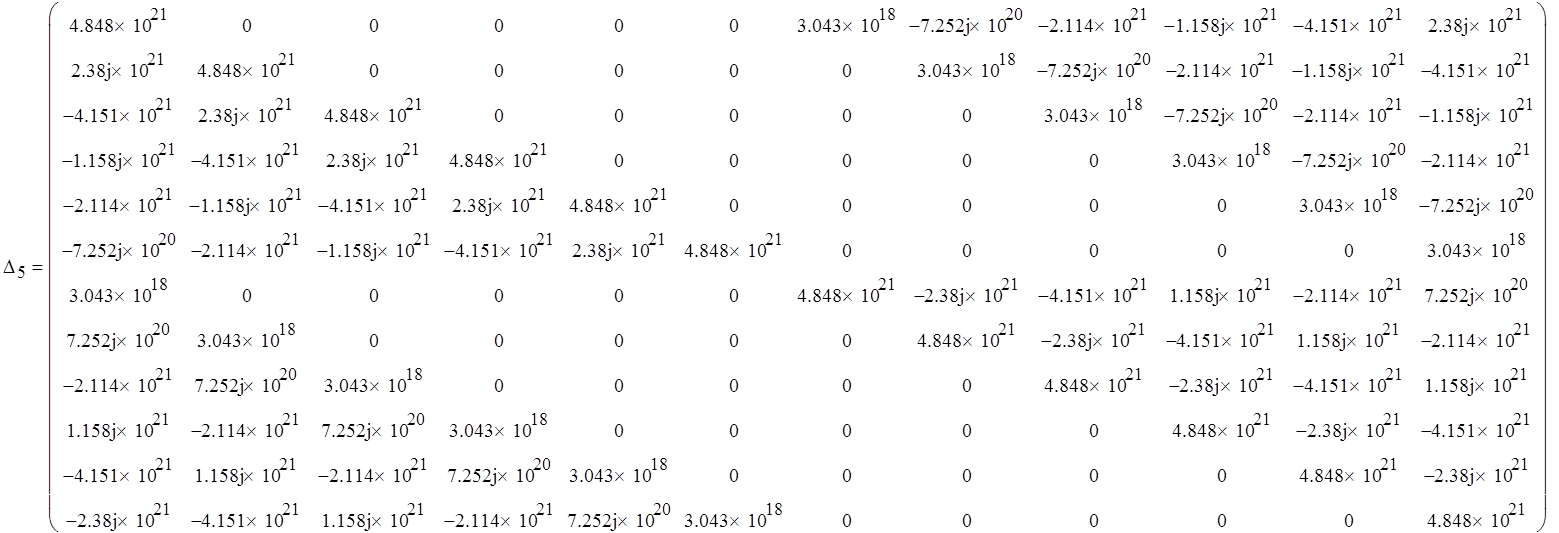
Вычислим определители:

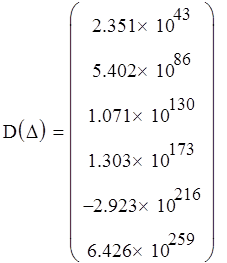
Так как знаки определителей на четных и нечетных местах не чередуются, дискретная система неустойчива.