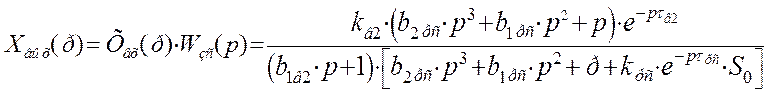
Воспользуемся теоремой о конечном значении оригинала для определения установившегося значения в переходном процессе замкнутой системы автоматического регулирования по каналу возмущения с И - регулятором:
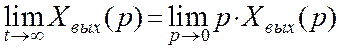
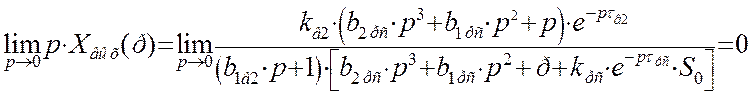
При анализе переходного процесса по второму каналу возмущения на возможное появление статической ошибки установлено следующее:
![]()
Квадратичная
интегральная оценка 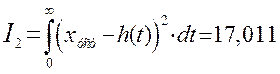
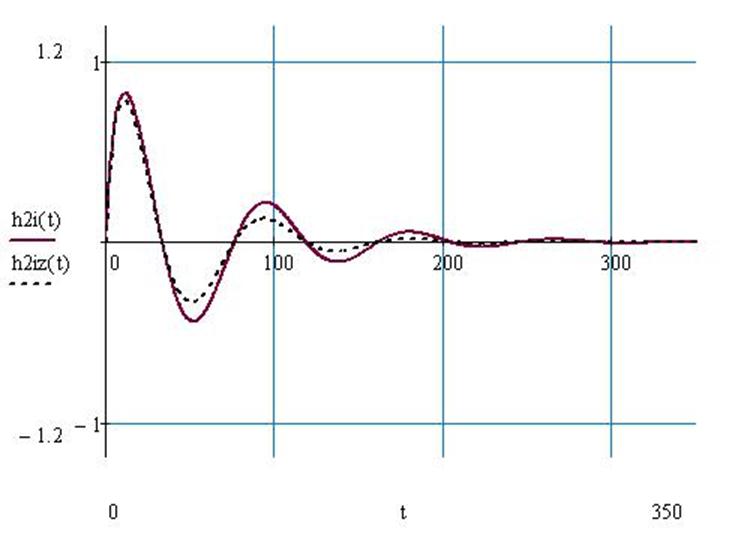
Рис.71 Переходный процесс по второму каналу возмущения в системе с И – регулятором без запаздывания и с запаздыванием.
Передаточная функция замкнутой системы по второму каналу возмущения с П – регулятором примет следующий вид:
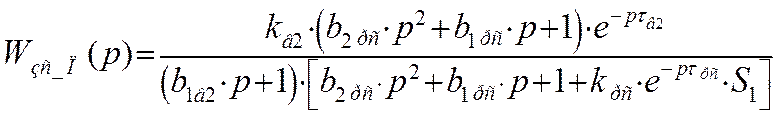
Найдем изображение переходной функции замкнутой системы:
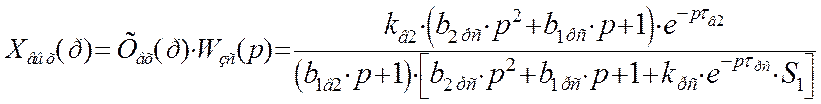
Воспользуемся теоремой о конечном значении оригинала для определения установившегося значения в переходном процессе замкнутой системы автоматического регулирования по каналу возмущения с И - регулятором:
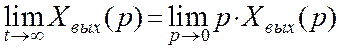
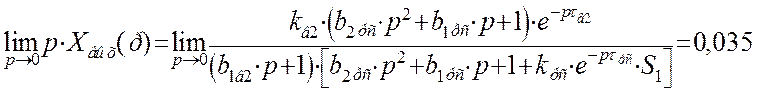
При анализе переходного процесса по второму каналу возмущения на возможное появление статической ошибки установлено следующее:
![]()
Квадратичная
интегральная оценка 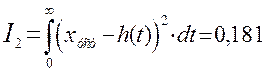
Рис.72 Переходный процесс по второму каналу возмущения в системе с П – регулятором без запаздывания и с запаздыванием.
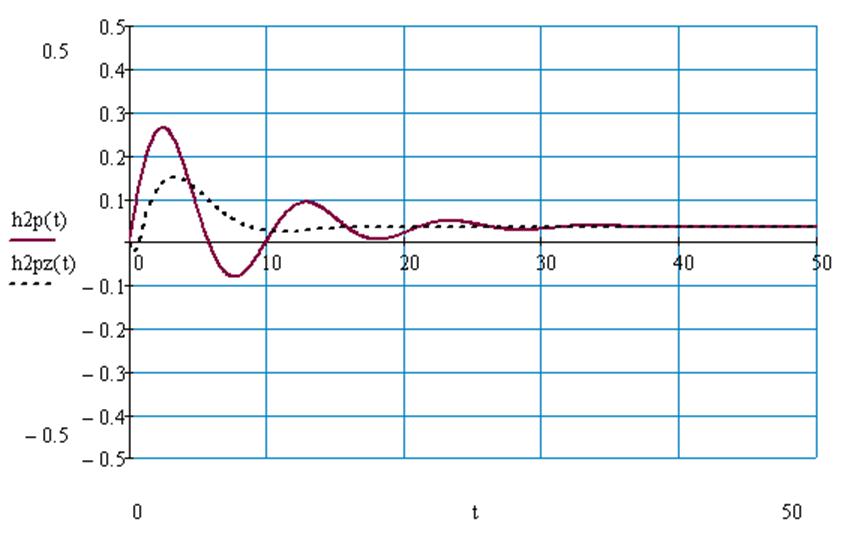
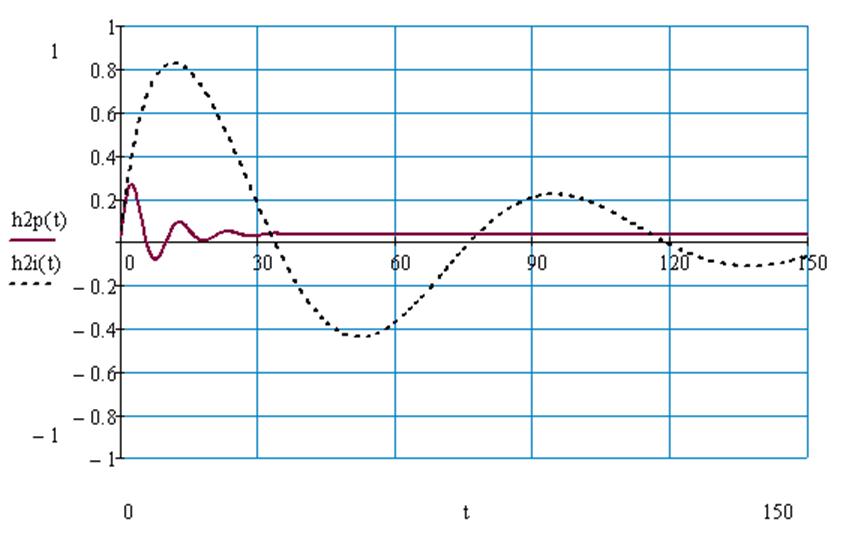
Рис.73 Переходный процесс по второму каналу возмущения в системе с И регулятором и в системе с П регулятором без запаздывания.
Для построения переходного процесса в замкнутой системе по третьему каналу возмущения вновь применим последовательность ранее поделанных преобразований:
Передаточная функция замкнутой системы по третьему каналу возмущения с И – регулятором примет следующий вид:
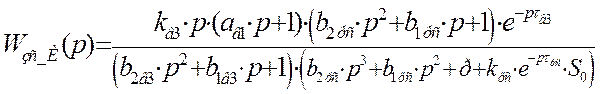
Найдем изображение переходной функции замкнутой системы:
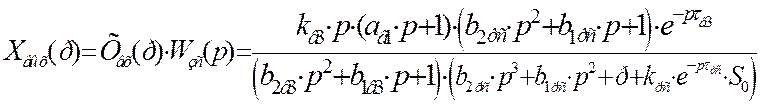
Воспользуемся теоремой о конечном значении оригинала для определения установившегося значения в переходном процессе замкнутой системы автоматического регулирования по каналу возмущения:
![]()
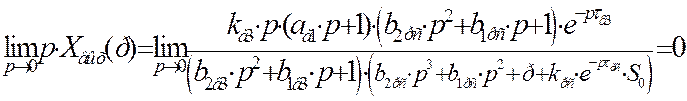
При анализе переходного процесса по третьему каналу возмущения на возможное появление статической ошибки установлено следующее:
![]()
Квадратичная
интегральная оценка 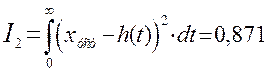
Рис.74 Переходный процесс по третьему каналу возмущения в системе с И – регулятором без запаздывания и с запаздыванием.
Передаточная функция замкнутой системы по третьему каналу возмущения с П – регулятором примет следующий вид:
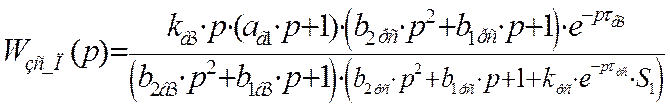
Найдем изображение переходной функции замкнутой системы:
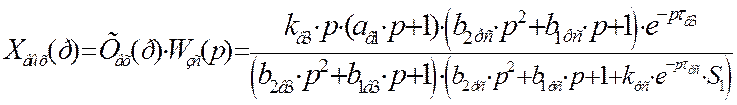
Воспользуемся теоремой о конечном значении оригинала для определения установившегося значения в переходном процессе замкнутой системы автоматического регулирования по каналу возмущения:
![]()
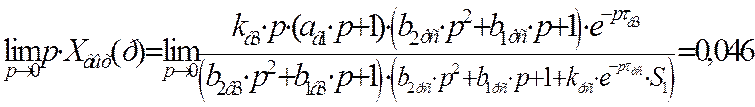
При анализе переходного процесса по третьему каналу возмущения на возможное появление статической ошибки установлено следующее:
![]()
Квадратичная
интегральная оценка 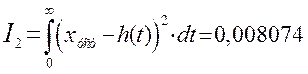
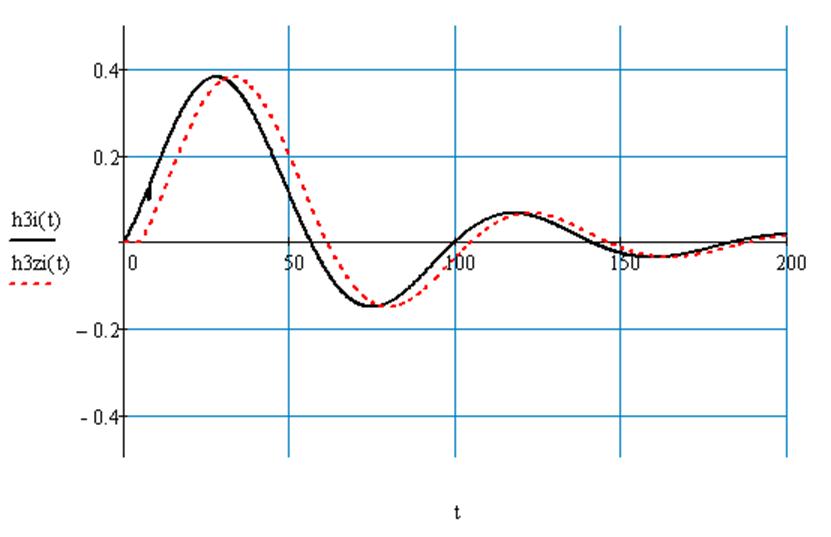
Рис.75 Переходный процесс по третьему каналу возмущения в системе с П – регулятором без запаздывания и с запаздыванием.
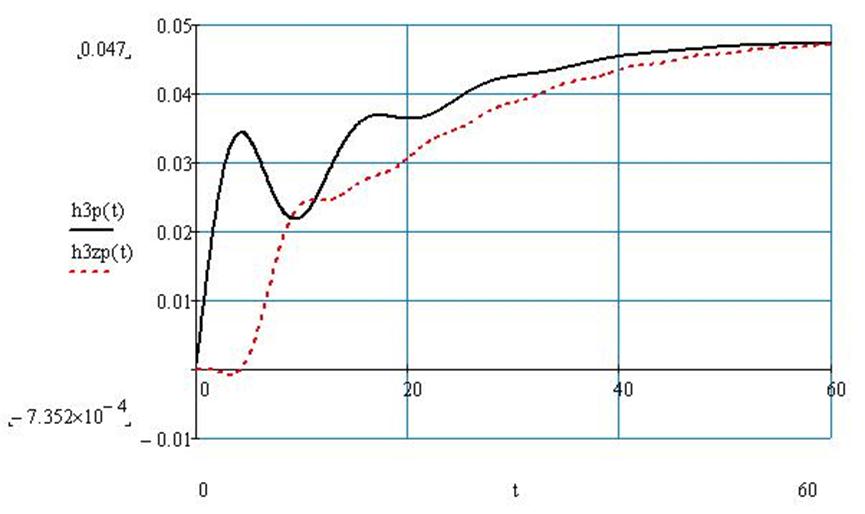
Рис.76 Переходный процесс по третьему каналу возмущения в системе с И регулятором и в системе с П регулятором без запаздывания.
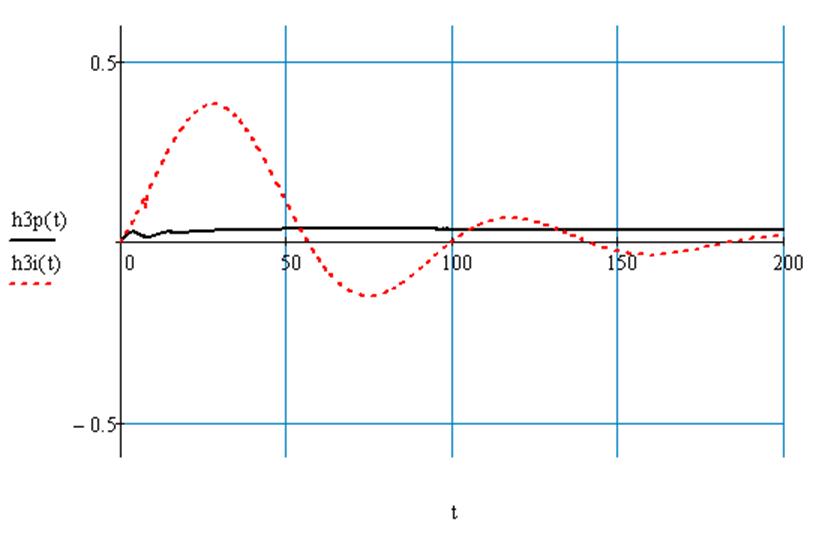
3.4 Определение нулей и полюсов передаточных функций замкнутой системы с И – регулятором и с П - регулятором по каналам управления и возмущения
Для получения корневых показателей качества системы управления необходимо рассчитать корни полиномов числителя и знаменателя передаточной функции замкнутой системы для случаев, когда запаздывание в канале регулирования объекта равно нулю.
Передаточную функцию замкнутой системы в общем виде можно представить в виде отношения передаточных функций разомкнутой системы:
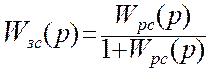
Передаточную функцию разомкнутой системы представим в виде произведения передаточных функций объекта и И-регулятора:
![]() где
где 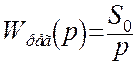
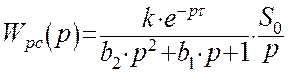
С учетом отсутствия запаздывания по каналу регулирования, подставим выражение полученное в формулу передаточной функции замкнутой системы и получим передаточную функцию замкнутой системы в виде отношения полиномов числителя и знаменателя:
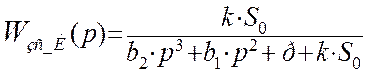
Полюса передаточной функции найдем, приравняв характеристический полином к нулю:
![]()
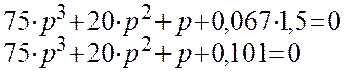
Вычисляя это
характеристическое уравнение на компьютере, получим решение:
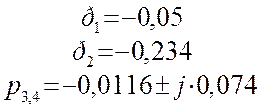
Нулей у передаточной функции нет.
Рис. 77 Нули и полюса передаточной функции замкнутой
системы по каналу регулирования с И – регулятором.
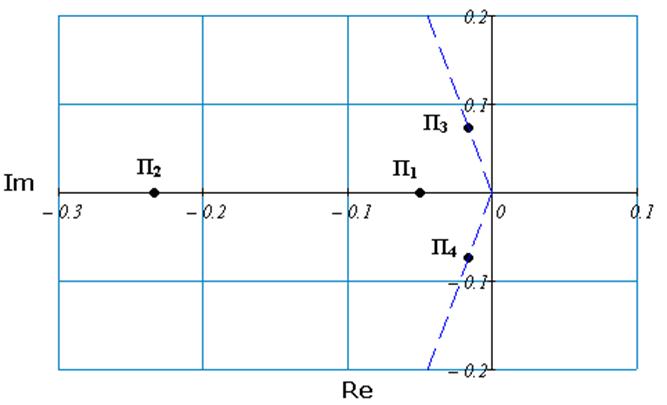
Доминирующими полюсами являются П3 и П4. Уменьшение амплитуды колебательной составляющей, создаваемое комплексными полюсами П3 и П4 зависит от модуля вещественной составляющей этих полюсов. Время регулирования переходной характеристики зависит от абсолютного значения вещественной части доминирующих полюсов. Полюса П1, П2 оказывают малое влияние из-за удаленности от мнимой оси. Нулей нет.
Передаточную функцию разомкнутой системы представим в виде произведения передаточных функций объекта и П-регулятора:
![]() где
где ![]()
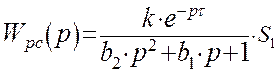
С учетом отсутствия запаздывания по каналу регулирования, подставим выражение полученное в формулу передаточной функции замкнутой системы и получим передаточную функцию замкнутой системы в виде отношения полиномов числителя и знаменателя:
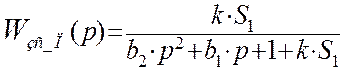
Полюса передаточной функции найдем, приравняв характеристический полином к нулю:
![]()
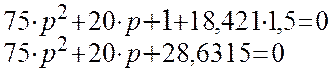
Вычисляя это
характеристическое уравнение на компьютере, получим решение:
![]()
Нулей у передаточной функции нет.
Рис. 78 Нули и полюса передаточной функции замкнутой
системы по каналу регулирования с П – регулятором.
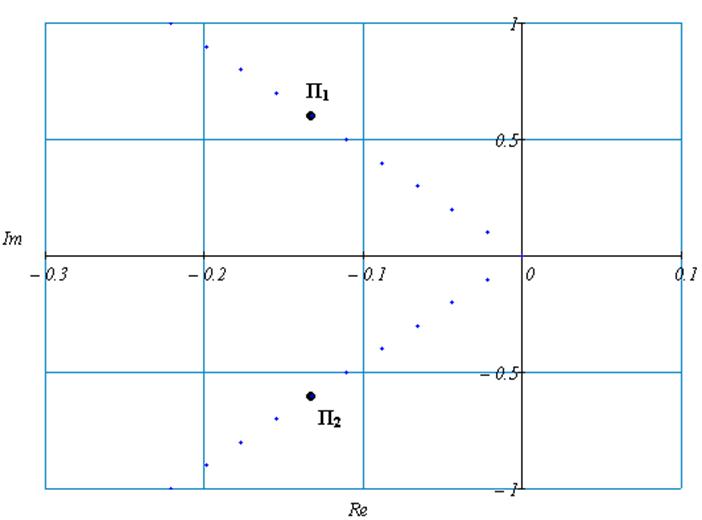
Доминирующими полюсами являются П1 и П2. Уменьшение амплитуды колебательной составляющей, создаваемое комплексными полюсами П1 и П2 зависит от модуля вещественной составляющей этих полюсов. Время регулирования переходной характеристики зависит от абсолютного значения вещественной части доминирующих полюсов. Нулей нет.
Для нахождения нулей и полюсов передаточной функции замкнутой системы по первому каналу возмущения в выражении передаточной функции замкнутой системы приравняем числитель и знаменатель к нулю.
Полюса передаточной функции с И - регулятором найдем, приравняв характеристический полином к нулю:
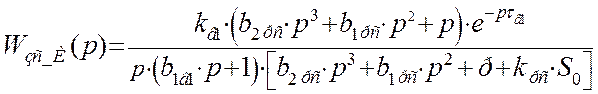
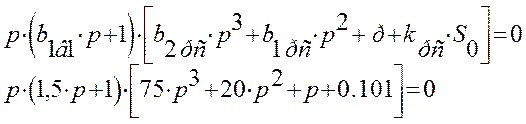
Вычисляя это характеристическое уравнение на компьютере,
получим решение: 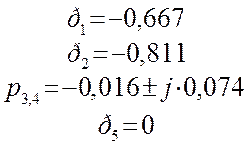
Нахождение нулей передаточной функции с И - регулятором сводиться к нахождению нулей полинома числителя, приравненного к нулю:
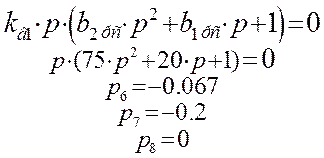
Рис.79 Нули и полюса передаточной функции замкнутой системы по первому каналу возмущения с И – регулятором.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.