Элементы математической логики. Нормальные виды формул. Совершенные нормальные формы, страница 23

Статистики и  являются несмещенными оценками неизвестной дисперсии .

 характеризует рассеивание групповых средних.

 характеризует рассеивание внутри групп.

Вводят статистику

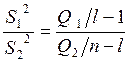
Такая статистика имеет распределение Фишера  и она используется для проверки гипотезы .

Гипотеза  не противоречит результатам наблюдений, если .

В этом случае оценки являются не  смещенными оценками математического ожидания. Если же , то гипотеза  отвергается и среди математических ожиданий  есть хотя бы 2 не равных.

Пример: Из большой группы полевых транзисторов с недельным интервалом полученной выборки и проведены результаты измерения емкости затвор-сток в пФ. На уровне значимости  проверить гипотезу об отсутствии влияния недельной работы на емкость.

2,8	3,2
3,2	3,1
2,9	3,4
3,5	3,0
3,3	3,6
3,7	3,1
3,9	3,2
3,1	3,2

Вычисление , и  удобнее проводить по формулам:

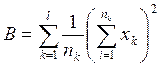
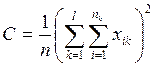
			Сумма
	2,8	3,2
	3,2	3,1
	2,9	3,4
	3,5	3,0
	3,3	3,6
	3,7	3,1
	3,9	3,2
	3,1	3,2
	8	8	16
	26,4	25,8	52,2
	88,14	83,46	171,6
	87,12	83,20	170,32

;

Гипотеза о равенстве математических ожиданий принимается.

Линейный множественный регрессионный анализ

Пусть случайные величины  и  зависимы и .

- -мерный случайный вектор

Компоненту  называют фактором

При проведении эксперимента фиксируют значения  и значения факторов и получают матрицу результатов.

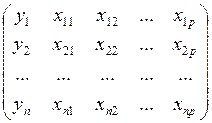
 − количество опытов

− число факторов

− значение на -том опыте -го фактора

Задача множественного регрессионного анализа состоит в построении такого уравнения плоскости в  пространстве, что отклонение наблюдаемого значения случайной величины  этой плоскости были бы минимальными. Т.е. следует найти такие значения коэффициента в линейном полиноме, чтобы выражение  было минимальным.

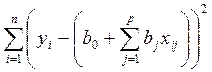 − min.

В случае :

Эти две прямые перпендикулярны в точке .

При  прямые перпендикулярны.

При  прямые параллельны.

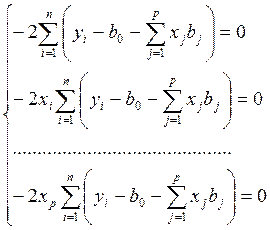
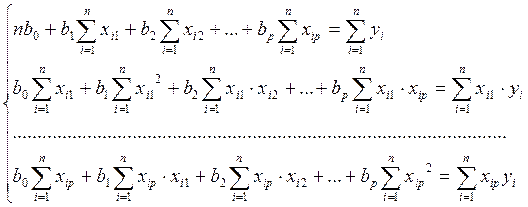
В матричном виде:

 ;

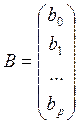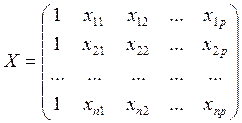
Это и есть решение системы относительно .

Тогда решение имеет вид:

 − коэффициент аппроксимирующего полинома.

Сложность:

Вычисления проводят только с применением быстродействующих ЭВМ. Теоретически точность аппроксимации можно было бы повысить, повышая степень полинома, но практически это не делают, т.к. при проведении матричных операций накапливается погрешность округления.

Проверка значимости регрессий проводится по схеме:

1)

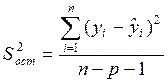
2) Считают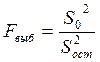

3) Выбирают уровень значимости .

4) Находят границу критической области по таблице распределения Фишера.

5) Если , то построенное уравнение регрессии хорошо предсказывает результаты опыта.

Схема проверки значимости коэффициентов :

1) Вычисляют погрешность коэффициента регрессии по формуле:

, где  − диагональные коэффициенты.

2) вычисляют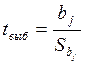

3) выбирают уровень значимости .

4) По таблице распределения Стьюдента находят

5) Если , то  коэффициент  является хорошим приближением.

Пусть  − значение коэффициента регрессии в генеральной совокупности, тогда доверительный интервал для  имеет вид: