Элементы математической логики. Нормальные виды формул. Совершенные нормальные формы, страница 22

                 (1)       − мера отклонения гипотетической функции распределения от эмпирической функции распределения.

Теорема Пирсона: Какова бы ни была функция распределения  случайной величины , распределение величины , при , стремиться к  распределению с числом степеней свободы , где  − число интервалов группировки и  − число параметров распределения.

На практике предельное распределение  используют при  и . В этом случае критическую границу выбирают  в точке .

Если наблюдаемое значение статистики, определенной формулой (1), удовлетворяет неравенству , то гипотезу  не противоречит результатам испытаний.

Пример:

Число отказов	0	1	2	3
Частота	42	10	4	3

Проверить гипотезу о том, что число отказов имеет распределение Пуассона. Уровень значимости .

Число отказов	Частота
0	42	0,63	37
1	10	0,29	17
2	4	0,07	4
3	3	0,01	1

0	42	0,63	37	0,68
1	10	0,29	17	2,88
	7	0,08	5	0,8

Число степеней свободы

 − три интервала группировки.

 − один параметр

По таблице надо найти значение .

Т.к. , то гипотеза  отклоняется.

Отсев грубых погрешностей измерений

Пусть есть выборка  некоторой случайной величины .

 − либо самое маленькое, либо самое большое из наблюдаемых значений.

Основная гипотеза : значение  аномально, т.е. есть грубая погрешность наблюдений. Конкурирующая гипотеза : значение  не аномально.

В качестве статистики используют статистику :

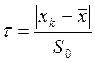
Задается вероятность . Известно, что критические значения  выражаются через критические значения распределения Стьюдента по формуле:

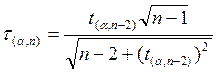
В качестве  выбирают 0,05 или 0,001.

По таблице распределения Стьюдента находят значения  и пересчитывают  и

По формуле 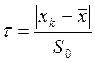 считаем  выборочное, предварительно вычислив  и .

а) Если , то гипотеза верна и такое значение  отбрасывается.

б) Если , то значение можно отбросить, если в пользу от силы есть и другие соображения в) Если , то гипотеза  отвергается и значение  отсеивать нельзя.

Пример:

Дана выборка. Произвести по ней отсев грубых погрешностей.

83, 78, 70, 61, 95, 65, 70, 78

Проверим число 75%

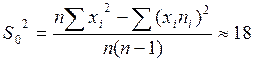
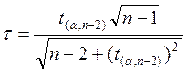
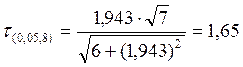
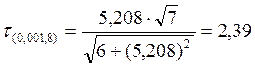
Значение  является грубой погрешностью измерения и его надо отбросить.

Замечания: после исключения того или иного наблюдения, характеристики должны быть пересчитаны по данным сокращенной выборки.

Однофакторный дисперсионный анализ

Однофакторный дисперсионный анализ применяют, чтобы установить оказывает ли существенное влияние фактор , который имеет  уровней на изучаемую случайную величину .

Пусть нормально распределенная случайная величина  наблюдается при  постоянных значениях некоторого фактора . В результате наблюдений составляют  групп объемом , принадлежащих  генеральным совокупностям, имеющих равные, но неизвестные дисперсии  и математические ожидания .

Проверяем гипотезу , которая говорит, что математические  ожидания равны.

 − -ое значение -ой группы

− выборочное среднее -ой группы

− обще среднее

− число элементов в -ой группе

,

Общая сумма квадратов отклонения наблюдения от   может быть представлена формулой:

Основное тождество дисперсионного анализа:

Если верна гипотеза  о равенстве математических ожиданий, то статистики  и  независимы и распределены по закону , первая статистика с , вторая с  степенями свободы.