Элементы математической логики. Нормальные виды формул. Совершенные нормальные формы, страница 2

3)  А  - тавтология тогда и только тогда, когда  тождественно ложно

4)  А - тождественно ложно тогда и только тогда, когда - тавтология

5)  - тавтология тогда и только тогда, когда А и В равносильны

Основные тавтологии:

1) - закон исключенного третьего

2)

3)

4)- цепное рассуждение

5)

6),

7)

8),  

9)

10) - закон Пирса

Основные равносильности:

1)                             - коммутативность конъюнкции

2)                                   - идемпотентность конъюнкции

3)          - ассоциативность конъюнкции

4)                             - коммутативность дизъюнкций

5)                                   - идемпотентность дизъюнкций

6)          - ассоциативность дизъюнкций

7) -дистрибутивность дизъюнкции относительно конъюнкции

8) -дистрибутивность конъюнкции относительно дизъюнкции

9)                          -первый закон поглощения

10)                        -второй закон поглощения

11)                                 -снятие двойного отрицания

12)                        -первый закон де Моргана

13)                        -второй закон де Моргана

14)               -первая формула расщепления

15)               -вторая формула расщепления

16)

17)

18)

19)

Правила преобразования:

1)  Если  и С - произвольная формула, то , , , , , .

Пример: , , тогда

2)  Пусть  и С – формула в которой выделено вхождение переменной . Пусть  получается заменой этого вхождения переменной  на  А, а   на B. Тогда

Пример: из равносильности  (№17) :

. Заменим  на . Тогда .

3)  Пусть  формула содержащая А в качестве своей подформулы, и пусть  получается заменой А на В, тогда, если , то .

Пример:  .

Пусть   –  и - подформула, тогда

           –  .

4)  Для каждой формулы можно указать равносильную ей, не содержащую логических символов  и .

Пример:

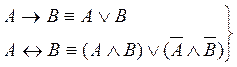 - основные формулы с помощью которых избавляются от импликации и эквиваленции.

.

Двойственность.

Определение: Символы  и  называются двойственными друг к другу. Формула  называется двойственной к формуле А, если она получена из А одновременной заменой всех символов  и  на двойственность. Очевидно, что .

Пример:

Утверждения:

1)  Пусть А – формула и  - набор переменных от которого она зависит. Тогда А принимает значение «истина» на каком-либо наборе тогда и только тогда, когда  принимает значение «ложь».

2)  Пусть , тогда

Нормальные виды формул.

Определение: Формулу называют элементарной конъюнкцией, если она является конъюнкцией переменных и отрицанием переменных. ( , , , ).

Определение: говорят, что формула находится в дизъюнктивной нормальной форме (ДНФ), если она является дизъюнкцией элементарных конъюнкций.

Теорема: Для любой формулы А существует формула В находящаяся в ДНФ такая, что .

Определение: Формулу называют элементарной дизъюнкцией, если она является дизъюнкцией переменных и отрицанием переменных. (,, ).

Определение: Формула находится в конъюнктивной нормальной форме (КНФ), если она является конъюнкцией элементарных дизъюнкций.

Теорема: Для любой формулы А существует такая формула В, что В находиться в КНФ и .

Определение: Функция двойственная элементарной конъюнкции является элементарной дизъюнкцией.

Определение: Формула А находится в КНФ, если двойственная к ней  определена и находится в ДНФ.

Пример:  

- Элементарная конъюнкция. Она находится в ДНФ и КНФ.

Пример: Привести к КНФ или ДНФ.

 - КНФ

Совершенные нормальные формы

Определение: Совершенной дизъюнктивной нормальной формой (СДНФ) данной формулы относительно переменных  называют такую ее ДНФ, в которой в каждой элементарной конъюнкции на R-том месте находится переменная  или ее отрицание.

 - СДНФ.

Алгоритм для табличного способа построения СДНФ:

1)  Составить таблицу истинности

2)  Выделяется строки, в которых формула принимает значение «истина»

3)  По каждой выделенной строке составляют элементарную конъюнкцию в которой переменная, принимающая истинностное значение «истина» входит без отрицания, а «ложь» с отрицанием.