Элементы математической логики. Нормальные виды формул. Совершенные нормальные формы, страница 16

.

Пример: Посчитать ковариацию.

	-1	1	3
1	0,2	0,1	0,1
2	0,3	0,2	0,1

	-1	1	3
	0,5	0,3	0,2

	1	2
	0,4	0,6

Если величины непрерывные, то:

Свойства ковариации:

1) Если  и  независимы, то ковариация равна 0.

2)

3)

4)

Определение: Матрицей ковариации называют матрицу вида:

Для случая  случайных величин, если  − случайный вектор, то для него существует матрица ковариации, элементы которой  определяются равенством:

  .

Получим, используя ковариацию, формулу для дисперсии линейной комбинации случайных величин  и  без предположения об их независимости.

 

Определение: коэффициентом корреляции случайной величины называется число .

Теорема: коэффициент корреляции удовлетворяет неравенству:

, причем если , то .

Доказательство:

.

Определение: Случайные величины  и для которых коэффициент корреляции  называются  некоррелированными.

Утверждение: из независимости случайных величин следует их некоррелированность, обратное – не верно.

Пример:

.

Пусть  − ДСВ, и пусть  − зависимы. Пусть

Определение: Функцию  называют наилучшим приближением  по методу наименьших квадратов, если  принимает наименьшее значение.

Определение: Функцию  называют среднеквадратичной регрессией  на .

Теорема: Линейная среднеквадратичная регрессия имеет вид:

Доказательство:

Рассмотрим

Функция от случайных величин.

Пусть

Определение: Функцией  случайной величины  называется суперпозиция функции  и функция  заданная на действительной оси , т.е. .

1) Пусть  − дискретная случайная величина, имеющая закон распределения и заданная не случайная функция, тогда  - также дискретная случайная величина.

Закон распределения: , где .

Пример: Пусть случайная величина задана таблицей. Написать закон распределения величины .

	-1	0	1	2
	0,2	0,3	0,1	0,4

	0	1	4
	0,3	0,3	0,4

2) Пусть  − непрерывная случайная величина.

 − функция распределения ее вероятности

 − ее плотность.

Пусть  − монотонно возрастающая непрерывная дифференцируемая функция, имеющая обратную: .

.

Тогда .

Пример: Дана плотность распределения  случайной величины , возможные значения которой распределены в интервале . Найти плотность распределения случайной величины .

Функция является строго возрастающей и существует обратная

, .

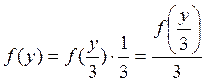Пусть  − монотонно убывающая функция, тогда:

                    (*)

Если не монотонная функция, то разбивают ее область определения на участки монотонности и на каждом участке по формуле (*) строят .

Пример: Пусть случайная величина  распределена нормально с параметрами  и . Найти плотность распределения случайной величины .

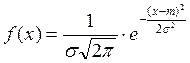
 − монотонно возрастающая на всей числовой оси функция. Для нее существует обратная функция:

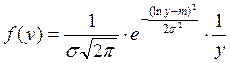
Определение: Такой закон распределения называется логарифмическим нормальным законом распределения. Ему подчиняются размеры частиц при дроблении.

Рассмотрим частичный случай, когда случайная величина .

Определение: Семейство законов распределения, описываемых функцией распределения , где  − фиксированная функция распределения  и  называется видом распределения.

Параметр  называют параметром сдвига, параметр  − масштабным  множителем.

Утверждения: