Решение.Чтобы воспользоваться известными нам основными разложениями, перейдём
от ряда Тейлора к ряду Маклорена. Для этого рассмотрим новую переменную t = x–7.
Тогда 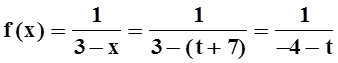 . С помощью несложных
преобразований и одного из основных разложений, найдём разложение функции
. С помощью несложных
преобразований и одного из основных разложений, найдём разложение функции ![]() в ряд Маклорена:
в ряд Маклорена:
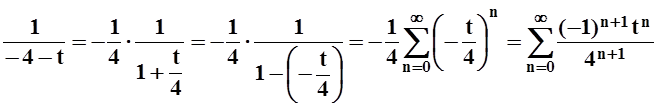 .
.
Теперь возвратимся к старой переменной х:
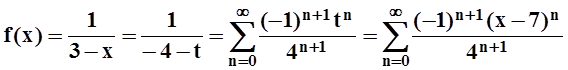 .
.
Так как формула для суммы
геометрической прогрессии, которой мы воспользовались, справедлива, если
знаменатель 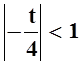 , то полученное разложение
справедливо при
, то полученное разложение
справедливо при
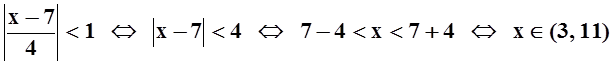 .
.
4. Написать 3 первых ненулевых члена разложения в ряд Маклорена функции y = ln(ex+x).
Решение. Будем последовательно вычислять y(0), y¢(0), y²(0), .... Нам нужно найти 3 первых ненулевых члена этой последовательности.
y(0) = ln(e0+0) = ln 1 = 0;
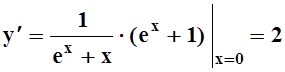 ;
;
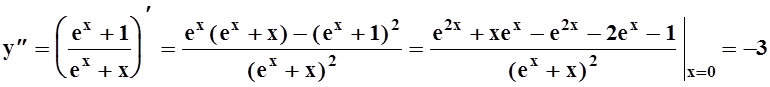 ;
;
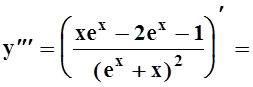
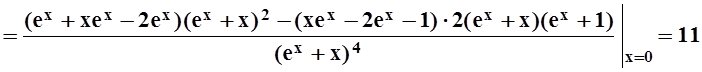 .
.
Подставляя в общую формулу ряда Маклорена, получим:
![]()
![]() .
.
5. Вычислить приближённо arctg 0,25 с точностью до 0,001.
Решение. Используем полученное в примере 11 разложение арктангенса в ряд Маклорена:
![]() .
.
Подставим ![]() :
:
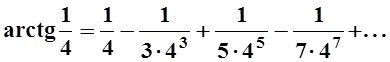 . Полученный ряд удовлетворяет
условиям теоремы Лейбница. Поэтому найдём слагаемое, которое меньше 0,001 и
отбросим его и следующие за ним:
. Полученный ряд удовлетворяет
условиям теоремы Лейбница. Поэтому найдём слагаемое, которое меньше 0,001 и
отбросим его и следующие за ним:
![]() .
.
14.6 Упражнения для самостоятельной работы
1. Найти область сходимости следующих рядов:
а) 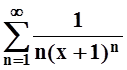 ; б)
; б) 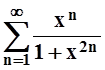 ;
;
в) 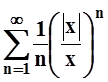 ;
г)
;
г) 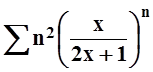 .
.
2. Найти радиус и интервал сходимости, исследовать сходимость в граничных точках для следующих степенных рядов:
а) 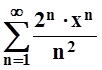 ;
б)
;
б) 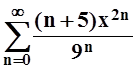 ;
;
в) 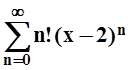 ; г)
; г)
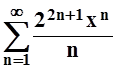 ;
;
д) 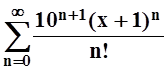 ; е)
; е) 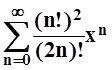 ;
;
ж)  ; з)
; з) 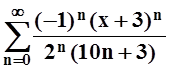 .
.
3. Найти
круг сходимости (без исследования на границе) для степенных рядов в поле
комплексных чисел: а) 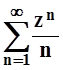
![]() ;
б)
;
б) 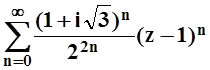 ;
;
в) ![]() ; г)
; г) ![]() .
.
4. Построив мажорирующие ряды, доказать равномерную сходимость на указанных промежутках следующих степенных рядов:
а) 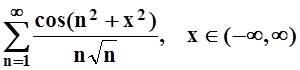 ; б)
; б) 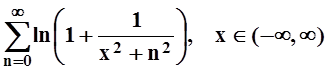 ;
;
в) 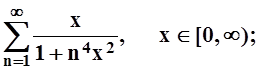 г)
г) ![]() .
.
5. Разложить функции в ряд Тейлора в окрестности точки х0. Указать интервалы, на которых справедливы полученные разложения.
а) ![]() ; б) f(x) = ln x , x0 = 4 ;
; б) f(x) = ln x , x0 = 4 ;
в) f(x) = sin 3x ,
x0 = p
; г) ![]() .
.
6. Разложить функции в ряд Маклорена. Указать интервалы, которых справедливы полученные разложения.
а) f(x) = (1+x)ln(1+x) ; б) f(x) = (ex+3)2 ;
в) ![]() ; г)
; г) 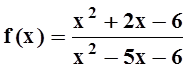 ;
;
д) f(x) = sh x ; е) f(x) = ln(15–2x–x2) ;
ж) f(x) = arcsin x ;
з) 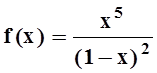 .
.
7. Написать 3 первых ненулевых члена разложения в ряд Маклорена следующих функций:
а) 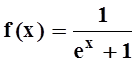 ;
б) f(x) = ex
cos x ;
;
б) f(x) = ex
cos x ;
в) ![]() ; г) f(x) = tg x.
; г) f(x) = tg x.
8. Вычислить приближённо (с погрешностью, не превышающей e) значения функций:
а) sin 3°, e= 0,0001; б) ln 1,3 , e= 0,001 ;
в) ![]() ; г)
cos 1,e= 0,001 ;
; г)
cos 1,e= 0,001 ;
д) ![]() ;
д)
;
д) ![]() .
.
9. Вычислить
приближённо (с погрешностью, не превышающей 0,001)
следующие интегралы: а) 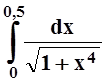 ;
б)
;
б) 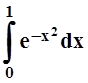 ;
;
в) 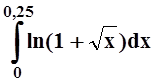 ; г)
; г)
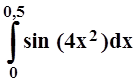 ;
;
14.7 Образец теста
(для дистанционной формы обучения).
1. Найти
область сходимости ряда 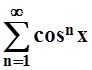 . В ответе
указать целое число, не лежащее в области сходимости.
. В ответе
указать целое число, не лежащее в области сходимости.
2. Найти
радиус сходимости ряда ![]() .
.
3. Ряд 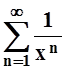 на промежутке [2, 3] 1)
сходится равномерно; 2) сходится поточечно, но не равномерно; 3) сходится
не во всех точках. Указать номер правильного ответа.
на промежутке [2, 3] 1)
сходится равномерно; 2) сходится поточечно, но не равномерно; 3) сходится
не во всех точках. Указать номер правильного ответа.
4. Найти
коэффициент при x4 в
разложении функции ![]() в ряд Маклорена.
в ряд Маклорена.
5. Сколько членов в разложении косинуса в ряд Маклорена нужно взять, чтобы вычислить cos 10° с ошибкой, не превышающей 0,0001 ?
6. Вычислить 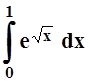 приближённо с точностью до 0,1
.
приближённо с точностью до 0,1
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.