Функциональные последовательности и ряды. Поточечная и равномерная сходимость, страница 8

Решение.Рассмотрим 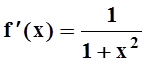. Разложение этой функции легко получить из  основного  разложения 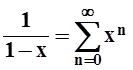    ,   если  перейти  к новой переменной по формуле  x = –t²:

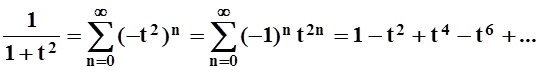
Ясно, что  xÎ(–1, 1) Û tÎ(–1, 1), поэтому разложение справедливо на интервале (–1, 1).  Проинтегрируем полученный ряд почленно на отрезке [0, x],  xÎ(–1, 1):

,

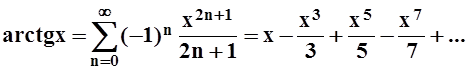
Разложение справедливо для  xÎ(–1, 1).

Подведём важные  с практической точки зрения итоги. Для решения задачи о разложении функции в степенной ряд есть 3 метода:

1) использование известных, основных разложений (см. примеры  9,10);

2) использование почленного дифференцирования или интегрирования (пример 11);

3) последовательное вычисление производных, т.е. использование определения ряда Тейлора. Так найдены разложения  e^x, sinx, (1+x)^a. Обычно это наиболее трудоёмкий путь.

Замечание. Степенные ряды дают нам новый способ здания функции. Этим способом можно задавать и другие, неэлементарные функции. Мы получаем возможность работать (вычислять значения, дифференцировать, интегрировать) с такими важными функциями, как, например, интегральный синус:

.

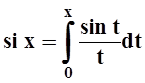Через элементарные функции этот интеграл не выражается. Очень удобно представить интегральный синус в виде ряда.  Так как    ,    то

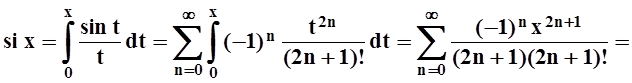
Многие применения степенных рядов основаны на том, что задание функции в виде суммы степенного ряда часто удобнее любого другого способа задания.

Мы рассмотрим на примерах 2 применения: приближённое вычисление значений функций и приближённое вычисление определённых интегралов.

Пример 12.  Вычислить приближённо    с точностью до   e= 0,001.

Решение. Заметим: 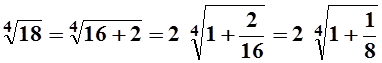. Рассмотрим функцию   ,   разложим её в степенной ряд:

.

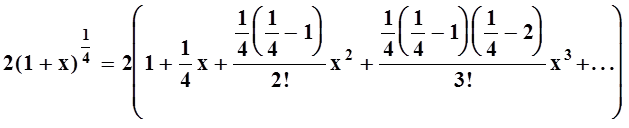Это биномиальное разложение справедливо, как мы знаем, при  xÎ(–1, 1). Поэтому можно применить его при   :

Знаки слагаемых (кроме первого) чередуются. Кроме того, модули слагаемых убывают:

неравенство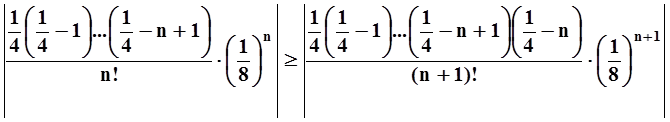 

равносильно очевидному неравенству 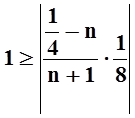 .  По теореме Лейбница, погрешность, допускаемая при замене суммы такого ряда частичной суммой, не превышает первого отброшенного слагаемого. Поэтому четвёртое слагаемое уже можно отбросить:

.

Промежуточные вычисления выполняются с одним запасным знаком.

Пример 13. Вычислить 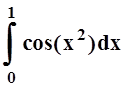     с точностью до   e= 0,001.

Решение. Разложим подинтегральную функцию в ряд Маклорена. Так как 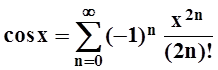,    то     .        Следовательно

.

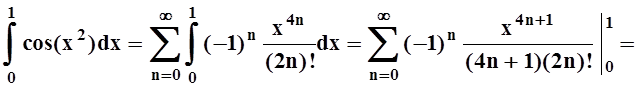
Обратите внимание: в примерах 12, 13 мы могли добиться любой требуемой точности.

14.5  Задачи с решениями

1.  Найти область сходимости ряда   .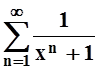

Решение.  Если | x | < 1 , то  ,  а значит 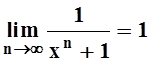 , и ряд расходится, так как нарушено необходимое условие сходимости. По этой же причине ряд расходится при  | x | = 1.

Пусть теперь  | x | > 1. Рассмотрим ряд 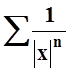 .  По признаку Коши он сходится, так как 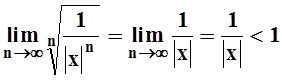   .  Применим предельный признак сравнения к рядам    ,    :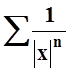

.

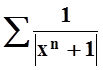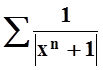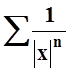Так как получилось конечное ненулевое число, то ряд  сходится – потому что   сходится.  Следовательно,  при таких  же  х   сходится  и  ряд    .

Ответ: областью сходимости ряда      является множество   (–¥, –1) È (1, ¥) .

2.  Найти круг сходимости степенного ряда 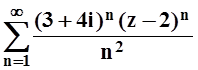  в поле комплексных чисел.

Решение.  Рассмотрим ряд с положительными действительными слагаемыми:

.

Применим к нему признак Даламбера:

.

Если 5| z–2 | < 1,то рядсходится. Это неравенство определяет круг  радиуса  с центром в точке  z = 2.

Так как из сходимости «ряда из модулей» следует сходимость самого ряда, то внутри найденного круга ряд сходится (абсолютно). Вне круга ряд расходится. На границе могут быть разные случаи. Однако для данного ряда исследование сходимости на границе провести легко: если , то | (3+4i)ⁿ(z–2)ⁿ | = 1    и ряд из модулей имеет вид : 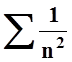, т.е.  сходится.  Значит, ряд сходится абсолютно на замкнутом круге  .

3.  Разложить функцию  в ряд Тейлора в окрестности точки x₀ = 7. Указать интервал,  на котором справедливо полученное разложение.