Функциональные последовательности и ряды. Поточечная и равномерная сходимость, страница 3

.

Теперь ясно, что

.

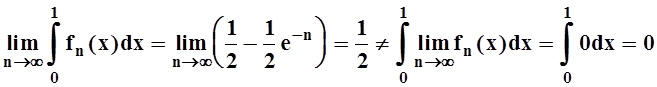Заключение теоремы 4 не выполнено. Значит, сходимость  f_n(x) ® 0  не является равномерной (на отрезке [0, 1]).

Мы будем чаще применять доказанную теорему 4 для функциональных рядов. Приведём соответствующую формулировку.

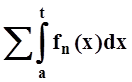Теорема 4¢(о почленном интегрировании ряда). Пусть функции  f_n(x) непрерывны на отрезке [a, b], причём ряд   равномерно сходится на [a, b] к сумме S(x). Тогда ряд  равномерно сходится на  [a, b]  к сумме  .  В частности,

.

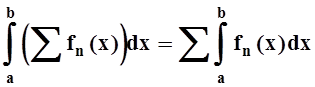Пример 5. Рассмотрим ряд 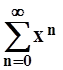, его слагаемые – непрерывные функции. Областью сходимости этого ряда является интервал  (–1, 1). Действительно, для каждого xÎ(–1, 1) ряд представляет собой сумму бесконечно убывающей геометрической прогрессии. Как известно,

.

На концах интервала (–1, 1), а также вне него ряд расходится – нарушено необходимое условие сходимости.

Сходимость ряда 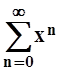 на интервале (–1, 1) не является равномерной. Действительно, частичная сумма     отличается от суммы всего ряда  S(x)  на величину

.

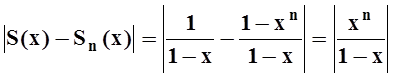Номер n₀, начиная с которого эта величина становится меньше заданного e, зависит от х. Чем ближе  х  к  1,  тем больше приходится брать  n₀.  Сходимость неравномерная.

Теперь рассмотрим отрезок [–q, q] , где 0<q<1. На таком отрезке ряд 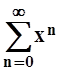  является мажорируемым:

| xⁿ | £  qⁿ.

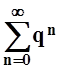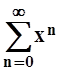Числовой ряд сходится. Поэтому, по признаку Вейерштрасса,  ряд  сходится равномерно. По теореме 4¢, его можно почленно интегрировать.  Интегрируя, например, по отрезку  [0, t] ,  где  0 < t £ q,  получим:

,

,

.

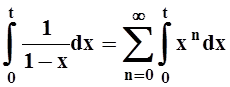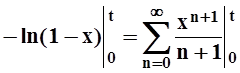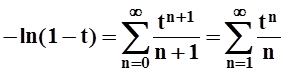Таким образом, мы нашли сумму ряда, рассмотренного выше в примере 2.

Изучим вопрос о почленном дифференцировании.

Теорема 5. Пусть функции f_n(x) непрерывно дифференцируемы на отрезке [a, b], причём

1) $x₀ Î[a, b]:   последовательность  f_n(x₀)  сходится ;

2) последовательность  f¢_n(x) сходится равномерно на [a, b] к некоторой функции u(x).

Тогда последовательность f_n(x) сходится равномерно на  [a, b] к некоторой функции  f(x), причём  f ¢(x) = u(x).

Другими словами, при определённых условиях производная от предельной функции равна пределу производных.

Доказательство. Для последовательности производных f¢_n(x) выполнены все условия теоремы 4. Значит, 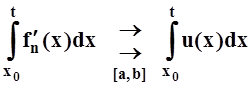 . Вычисляя интеграл в левой части: 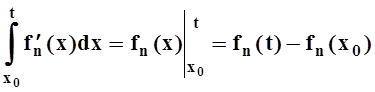,  получим:  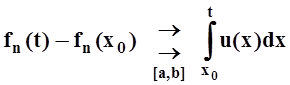.  По определению, это значит:

.

С другой стороны, по условию последовательность f_n(x₀) имеет предел. Обозначим его буквой  с.   Тогда   .

Рассмотрим функцию

и докажем, что она искомая, т.е.    и   f ¢(t) = u(t). Второе – очевидно; по теореме Барроу о производной интеграла с переменным верхним пределом:

.

Чтобы доказать равномерную сходимость , для данного e>0 рассмотрим  n₀ = max(n₁,n₂).  Тогда, при  n ³ n₀  справедливы полученные выше неравенства, а значит

.

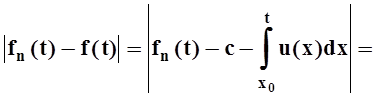
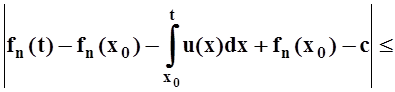
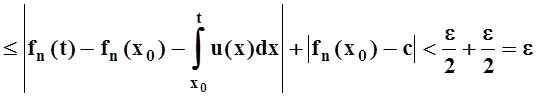Так как номер  n₀  выбирается независимо от  t,  то равномерная сходимость доказана.

Теорема 5¢(о почленном дифференцировании ряда). Пусть функции f_n(x) непрерывно дифференцируемы на  [a, b],  причём

1)  $x₀Î[a, b] :   числовой ряд    сходится ;

2)  ряд      равномерно сходится на   [a, b].

Тогда    тоже равномерно сходится, причём

.

14.3  Степенные ряды

Здесь мы применим полученные знания о функциональных рядах к важному частному случаю – случаю степенных рядов. Степенным рядом называется функциональный ряд вида

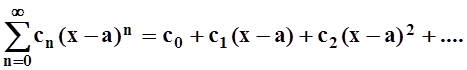
Числа  c_n,  n = 0,1,2,... называются коэффициентами ряда. Наиболее простой вид имеет степенной ряд, если  a = 0:

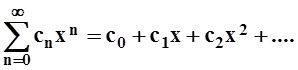
В дальнейшем можно работать только с такими рядами, так как общий случай сводится к случаю  a = 0  с помощью простой замены переменной:  x – a = t.

Теорема 6 (теорема Абеля). Если ряд  сходится при x = x₀, то он сходится (причём абсолютно) и при любом x₁:  | x₁| <| x₀ |.

Доказательство. По условию, числовой ряд   сходится. Поэтому  (необходимое условие сходимости). Так как любая сходящаяся числовая последовательность ограничена, то

$M :  | c_n x₀ⁿ| £ M    ("n).