Тэорыя лімітаў. Бясконца малыя і бясконца вялікія паслядоўнасці. Збежныя паслядоўнасці, страница 5

Далей разгледзім паслядоўнасць  пры кожным фіксаваным  з агульным элементам

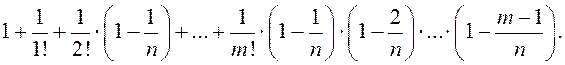
Зразумела,што што пры  маем

,                                                (7)

дзе 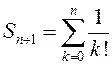. Паколькі , а , то пасля пераходу да ліміту ў роўнасці (7) пры  атрымаем

.                                          (8)

Пераходзячы ў (8) да ліміту пры , маем , адкуль . Формула (5) даказана. à

4°. Укладзеныя адрэзкі.

     def: Паслядоўнасць адрэзкаў лікавай прамой  такіх, што называецца паслядоўнасцю ўкладзеных адрэзкаў. Пры гэтым праўдзяцца няроўнасці

.                                       (9)

Тэарэма 2. (пра ўкладзеныя адрэзкі). Для ўсякай паслядоўнасці ўкладзеных адрэзкаў існуе пункт, які належыць усім адрэзкам паслядоўнасці.

□ З няроўнасцяў (9) вынікае, што лікавая паслядоўнасць  ёсць неспадальная і абмежаваная зверху, паколькі , а таму мае ліміт . Аналагічна  – ненарастальная і абмежаваная знізу паколькі , і таму існуе . Згодна з тэарэмаю пра лімітавы пераход у няроўнасцях маем . Такім чынам, кожны пункт  адпавядае ўмовам тэарэмы.   ■

def:Калі выконваецца роўнасць , то паслядоўнасць адрэзкаў з умоваю (9) называецца паслядоўнасцю сцягвальных адрэзкаў.

Тэарэма 3. (пра сцягвальныя адрэзкі). Для ўсякай паслядоўнасці сцягвальных адрэзкаў існуе адзіны пункт, які належыць усім адрэзкам паслядоўнасці.

□ З тэарэмы пра ўкладзеныя адрэзкі вынікае, што   і   ,  а таму маем  . Гэта і азначае, што пункт , які належыць усім адрэзкам ёсць адзіны, прычым .  ■

Практыкаванне1. Дайце прыклады паслядоўнасці укладзеных і паслядоўнасці сцягвальных адрэзкаў. ( , ).

Практыкаванне2. Разгледзім паслядоўнасцю сцягвальных інтэрвалаў . Ці маюць гэтыя інтэрвалы супольны пункт? Так, гэта пункт 0. Чаму ж мы не фармулюем тэарэму пра ўкладзеныя інтэрвалы? Таму што тэарэма непраўдзівая, калі замест адрэзкаў разглядаць інтэрвалы.

Напрыклад, для паслядоўнасці укладзеных інтэрвалаў , г.зн.

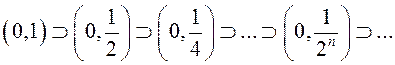
не існуе пункт, які належыць усім інтэрвалам. Сапраўды, які б пункт  з інтэрвала (0,1) мы ні ўзялі, заўсёды знойдзецца такі нумар  , што . Тада  , г.зн. . Такім чынам, пункт  не належыць бясконцаму мноству  інтэрвалаў разгляданай паслядоўнасці.

§2.4. Падпаслядоўнасці.

def: Няхай  ёсць некаторая лікавая паслядоўнасць, а  адвольная нарастальная паслядоўнасць натуральных лікаў, г.зн.  прычым  Паслядоўнасць , агульны элемент якой , г.зн. паслядоўнасць  называюць падпаслядоўнасцю лікавай паслядоўнасці . Такім чынам, калі з паслядоўнасці  выбраць элементы з нумарамі , то атрымецца падпаслядоўнасць . Калі падпаслядоўнасць  збежная, то яе ліміт называецца частковым лімітам паслядоўнасці .

Прыклад.  1) Няхай , тады , або  , , ..., што раўназначна адкіданню дзесяці першых элементаў паслядоўнасці.

2) Калі , то , г.зн. , ,...– з паслядоўнасці выбраны элементы з цотнымі нумарамі.

Тэарэма 1. Калі лікавая паслядоўнасць  збежная, то кожная яе падпаслядоўнасць  таксама збежная і мае той самы ліміт, што і .

□ Няхай , г.зн.  , а   адвольня яе падпаслядоўнасць. Паколькі , то пры  таксама , а таму , што і азначае збежнасць падпаслядоўнасці  да ліміту . ■

Заўвага 1. Калі паслядоўнасць мае два розныя частковыя ліміты, то сама паслядоўнасць ёсць разбежная.

Напрыклад, паслядоўнасць  мае дзве падпаслядоўнасці   і таму яна разбежная.

Тэарэма 2 (Бальцана-Ваерштраса або прынцып выбару). З кожнай абмежаванай лікавай паслядоўнасці можна вылучыць збежную падпаслядоўнасць.

□ Няхай паслядоўнасць  абмежаваная, г.зн , або  . Абазначым гэты адрэзак  і падзелім яго папалам. Тую яго палову, якая змяшчае бясконца многа элементаў паслядоўнасці  назавем , і гэты адрэзак зноў падзелім папалам. Такім чынам, мы атрымаем паслядоўнасць укладзеных адрэзкаў , даўжыня якіх

                                                    (1)

імкнецца да нуля пры . На падставе тэарэмы пра сцягвальныя адрэзкі існуе адзіны пункт  такі, што

                                                       (2)