Тэорыя лімітаў. Бясконца малыя і бясконца вялікія паслядоўнасці. Збежныя паслядоўнасці, страница 3

Атрымалі  ?!? . Гэта азначае, што лікавая паслядоўнасць   не мае ліміту, а тым самым ёсць разбежная.     ◄)

3º Сума [розніца] дзвюх збежных лікавых паслядоўнасцяў  і  ёсць збежная лікавая паслядоўнасць, якая мае лімітам суму [розніцу] лімітаў паслядоўнасцяў  і .

□ Няхай , , тады , , – бясконца малыя паслядоўнасці. А таму . Паколькі  ёсць бясконца малая паслядоўнасць, то .         ■

4º Здабытак  дзвюх збежных лікавых паслядоўнасцяў  і  ёсць збежная лікавая паслядоўнасць, якая мае лімітам здабытак лімітаў паслядоўнасцяў  і .

□ Няхай , , тады , , – бясконца малыя паслядоўнасці. А таму  . Паколькі  ёсць бясконца малая паслядоўнасць, то .   ■

5º (Ліміт дзелі дзвюх збежных лікавых паслядоўнасцяў.) Калі  і , то .

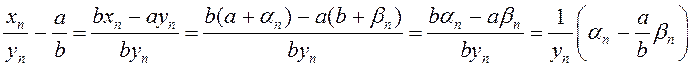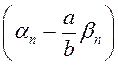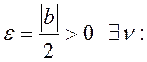
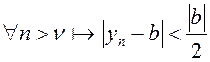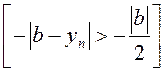
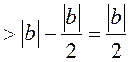□ Маем дзе – бясконца малыя паслядоўнасці. Таму . З уласцівасцяў бясконца малых паслядоўнасцяў вынікае, што  ёсць (бмп). Пакажам, што лікавая паслядоўнасць – абмежаваная. Паколькі  і , то для  . Далей атрымаем , г.зн. 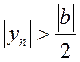, або 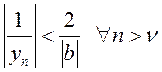, а таму – абмежаваная лікавая паслядоўнасць(Чаму?). Такім чынам, 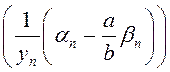– (бмп). Гэта значыць, мае месца выяўленне 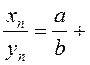(бмп). На падставе тэарэмы пра выяўленне збежнай паслядоўнасці маем .     ■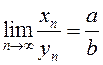

Прыклад 2. Вылічыць .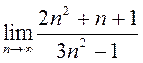

∆ . ◄

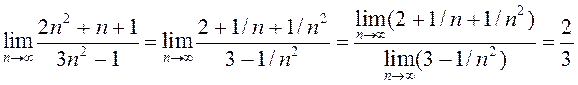6º Тэарэма 2. (пра лімітавы пераход у няроўнасцях). Калі, пачынаючы з некаторага нумара, для элементаў дзвюх збежных  лікавых паслядоўнасцяў  і  праўдзяцца няроўнасці , то ліміты гэтых паслядоўнасцяў праўдзяць няроўнасць  .

□ (ад процілеглага) Няхай , але . Возьмем лік  настолькі малы, каб праўдзілась няроўнасць

.                                                  (2)

(Дастаткова ўзяць .) Паколькі , то для выбранага ліку  зноўдзецца , што раўназначна няроўнасцям

                                                     (3)

.                                                    (4)

Выкарыстоўваючы па чарзе спачатку правую няроўнасць з (4), затым няроўнасць (2) і, нарэшце, левую няроўнасць з (3), атрымаем , адкуль вынікае, што    ?!?. А гэта і азначае, што .   ■

Заўвага 4. Для элементаў дзвюх збежных лікавых паслядоўнасцяў можа праўдзіцца строгая няроўнасць , але пры гэтым іх ліміты падпарадкоўваюцца нястрогай няроўнасці , г.зн. ліміты могуць быць роўнымі.  Напрыклад, для лікавых паслядоўнасцяў   мае месца няроўнасць , але .

7º Тэарэма 3. (пра сціснутую паслядоўнасць, або прынцып двух міліцыянтаў). Калі  мае месца няроўнасць

                                                                     (5)

 і , то і .

□ Выберам адвольна . Паколькі паслядоўнасці – збежныя, то  праўдзяцца няроўнасці

                                                      (6)

.                                                    (7)

Беручы адпаведныя няроўнасці з (6), (5) і (7), атрымаем

.

З гэтых няроўнасцяў вынікае , г.зн. .       ■

Прыклад 3. Даследаваць на збежнасць паслядоўнасць .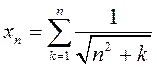

∆ Маюць месца наступныя ацэнкі 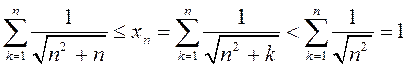, або 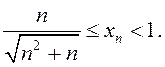 Паколькі 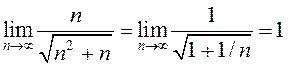, то, згодна з тэарэмаю пра сціснутую паслядоўнасць,

А цяпер інакш:

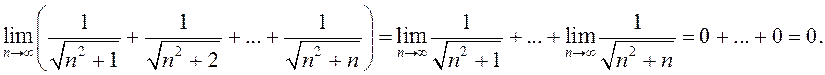Чаму атрымаўся іншы вынік?   ◄

§2.3. Манатонныя паслядоўнасці.

1°. Умова збежнасці манатоннай паслядоўнасці.

def: Лікавая паслядоўнасць  называецца нарастальнай, калі ; неспадальнай, калі ; спадальнай, калі ; ненарастальнай, калі . (Пры гэтым будзем іх абазначаць адпаведна .) Усе такія лікавыя паслядоўнасці называюцца манатоннымі (абазначаюцца ). Нарастальныя і спадальныя паслядоўнасці называюцца строга манатоннымі (абазначаюцца ).

Напрыклад,

1). (назавіце формулу агульнага элемента)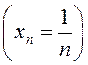– спадальная, абмежаваная лікавая паслядоўнасць;

2). 1; 1; 1/2; 1/2; ... 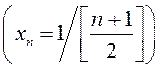– ненарастальная, абмежаваная;

3). 1/2; 2/3; 3/4; ... 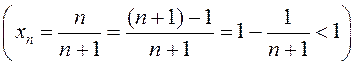– абмежаваная;

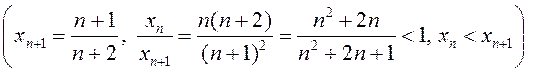–нарастальная.

Адзначым, што манатонныя паслядоўнасці абмежаваныя прынамсі з аднаго боку.

Тэарэма 1. (Крытэр збежнасці манатоннай паслядоўнасці). Для таго каб манатонная пас-лядоўнасць была збежнаю, неабходна і дастаткова, каб яна была абмежаванаю.

□ Неабходнасць. Абмежаванасць ёсць неабходная ўмова збежнасці ўсякай паслядоўнасці, у тым ліку манатоннай.