Математика \ Математический анализ

Тэорыя лімітаў. Бясконца малыя і бясконца вялікія паслядоўнасці. Збежныя паслядоўнасці, страница 11

Гіпербалічныя косінус і сінус праўдзяць раўнанне гіпербалы  (адсюль назва – гіпербалічныя функцыі), а менавіта мае месца тоеснасць    

12º. Адваротныя гіпербалічныя функцыі. Адваротную да функцыі  абазначаюць  Яна непарыўная як адваротная да непарыўнай функцыі. Атрымаем яе аналітычнае выяўленне. Дзеля гэтага развяжам раўнанне 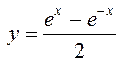 у дачыненні да x:

Паколькі , то  г.зн. .


 


Аналагічна атрымліваем

 


§2.12. Некалькі важных лімітаў.

Скарыстаем тэарэму пра непарыўнасць складанай функцыі, грунтоўны ступенева-паказнікавы ліміт і непарыўнасць асноўных элементарных функцый для вылічэння надалей важных наступных лімітаў.

1º.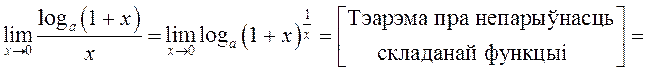

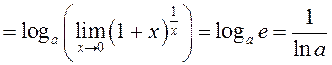. Такім чынам, маем

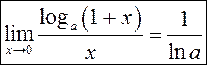 .      У прыватнасці     .

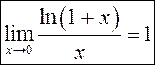2º. 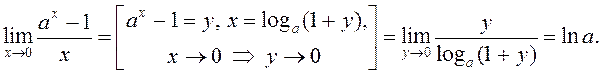 Маем

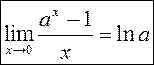 .    У прыватнасці       .

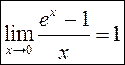3º.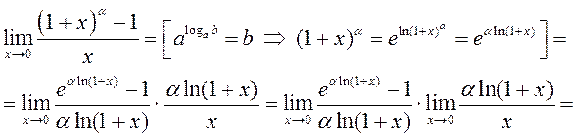

==

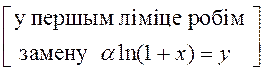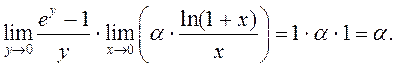
Такім чынам, атрымалі   

.

§2.13. Параўнанне функцый.

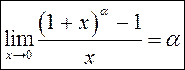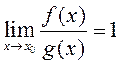def: Калі функцыі  і  вызначаны ў праколатай акрузе пункта  і , то функцыі  называюць эквівалентнымі ў акрузе пункта   і пішуць .

Напрыклад, 1)  таму, што  2) 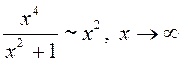 таму, што  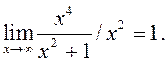3) (Чаму?)  4) (Чаму?)

Калі прыняць да ўвагі прыклады, разгледзеныя ў §§2.7 , 2.12, то можна скласці наступную табліцу эквівалентных функцый:


     ; ; ; ; .


Гэтыя стасункі застаюцца праўдзівымі, калі замяніць у іх xна бясконца малую функцыю

Напрыклад, ; ;                            ;   .

Геаметрычна эквівалентнасць азначае, што разгляданыя функцыі паводзяць сябе ў акрузе пункта  набліжана як адпаведныя прамыя:



.


Тэарэма 1. Калі функцыі  і  эквівалентныя ў акрузе пункта  і існуе , то існуе таксама .

□ Паколькі , то 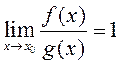, а тым самым .

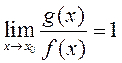Далей маем

    ■

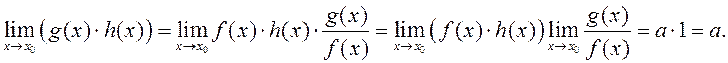Даказаная тэарэма дае магчымасць замяніць множнік (або дзельнік) пад знакам ліміту на эквівалентны яму множнік (або дзельнік).

Прыклад 1. Вылічыць .

∆ Выкарыстоўваючы непасрэдна грунтоўны трыганаметрычны ліміт, маем

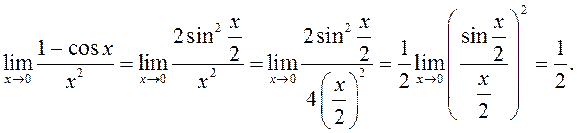
На падставе тэарэмы 1 атрымаем

 ◄

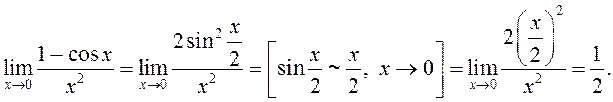Заўвага 1. З прыклада вынікае, што

.

Заўвага 2. Пры вылічэнні лімітаў складнікі нельга замяняць эквівалентнымі функцыямі. Сапраўды, калі ў прыкладзе 1, улічваючы , замяніць  на 1, атрымаем , што прывяло да непраўдзівага выніку.

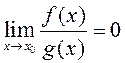def: Калі функцыі  і  вызначаны ў праколатай акрузе пункта  і , то функцыю  называюць бясконца малой у параўнанні з функцыяй  у акрузе пункта   і пішуць , .

Пры гэтым самі функцыі  і  могуць не быць бясконца малымі. Так 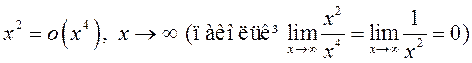, а функцыі  і  ёсць бясконца вялікія пры .

def: Калі  і , то кажуць, што функцыя  у акрузе пункта  ёсць бясконца малая больш высокага парадку, чым .

У сувязі з уведзеным абазначэннем часта выкарыстоўваецца запіс . Гэта азначае – бясконца малая ў пункце .

Адзначым наступныя ўласцівасці сымбаля  (тут ):

Тэарэма 2. (Пра выяўленне эквівалентных функцый). Для таго каб функцыі f(x) ig(x) былі эквівалентнымі ў акрузе пункта , неабходна і дастаткова, каб  

□ (Неабходнасць) Няхай . Згодна з азначэннем эквівалентнасці 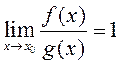. На падставе тэарэмы пра выяўленне функцыі, якая мае ліміт, 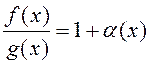, дзе . Такім чынам, .

Паколькі 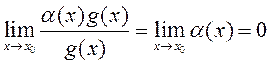, то , што і прыводзіць да роўнасці

(Дастатковасць) Няхай  Тады

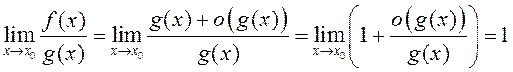, што і азначае .   ■

Гэты крытэр дазваляе пададзенай вышэй табліцы эквівалентных функцый надаць наступны выгляд:

            

;

;

;

 ; ;

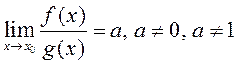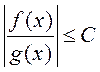def. Калі існуе канечны ліміт , то пішуць   Паколькі разгляданы ліміт ёсць канечны, то функцыя  абмежаваная ў акрузе пункта  , г.зн. , або . І таму пры гэтым таксама кажуць, што функцыя  абмежаваная ў параўнанні з функцыяй . Калі пры гэтым функцыі  і  ёсць бясконца малыя ў пункце , то кажуць, што  функцыі  і  маюць аднолькавы парадак малечыні.

Прыклад 2.

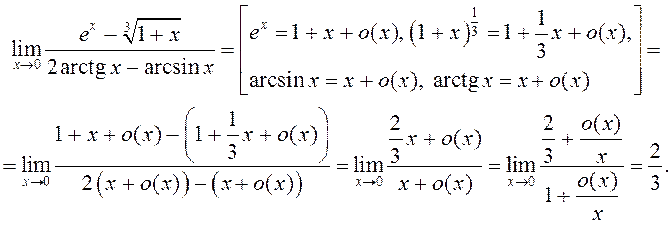
Прыклад 3.

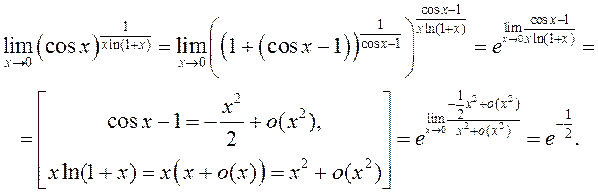
Трэба зазначыць, што выкарыстанне эквівалентных функцый не заўсёды прыводзіць да мэты.

Прыклад 4.  ?

Скачать файл