Тэорыя лімітаў. Бясконца малыя і бясконца вялікія паслядоўнасці. Збежныя паслядоўнасці, страница 2

4º. Калі лікавая паслядоўнасць  ёсць сталая і (бмп), то .

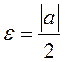□ Паколькі – (бмп), то   . Калі дапусціць, што , то пры  маем 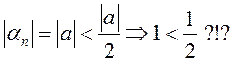  Такім чынам, .    ■

Прыклад. Пакажам, што лікавая паслядоўнасць  пры  – (бмп), а пры  ёсць (бвп).

∆ Калі , то паслядоўнасць ёсць (бмп) (уласцівасць 4°). Няхай . На падставе няроўнасці Бэрнулі ( , прычым роўнасць толькі пры ) маем  г.зн. лікавая паслядоўнасць  –(бмп) пры .  На падставе тэарэмы пра сувязь паміж (бмп) і (бвп) атрымліваецца, што  – (бвп) пры .◄ 

А што пры ? Пакуль пакінем без адказу.

§2.2. Збежныя паслядоўнасці.

def: Лікавая паслядоўнасць  называецца збежнай , калі існуе такі лік , што паслядоўнасць  ёсць (бмп), што раўназначна запісу . Пры гэтым пішуць  , або  і кажуць, што паслядоўнасць  мае ліміт . Калі такі лік  не існуе, то лікавая паслядоўнасць называецца разбежнаю.

Заўвага 1. Бясконца малая паслядоўнасць ёсць збежная паслядоўнасць, а яе ліміт роўны нулю.

Заўвага 2. Бясконца вялікая паслядоўнасць не мае ліміту. Калі  ёсць бясконца вялікая паслядоўнасць, то пішуць , або . Калі пры гэтым, пачынаючы з некаторага нумара, ўсе элементы лікавай паслядоўнасці дадатныя [адмоўныя], то пішуць  [].

Прыклад 1. Дакажам, што

∆ Разгледзім  Відочна, што  Возьмем . Такім чынам,  ◄

Тэарэма 1. (пра выяўленне збежнай лікавай паслядоўнасці). Для таго каб лікавая паслядоўнасць  мела лімітам лік  , неабходна і дастаткова, каб , дзе  ёсць бясконца малая паслядоўнасць .

□ (Неабходнасць) Няхай  і , то лікавая паслядоўнасць  ёсць бясконца малая паслядоўнасць. Гэта азначае, што мае месца выяўленне , дзе   – бясконца малая паслядоўнасць.

(Дастатковасць)  Няхай ,  – бясконца малая паслядоўнасць. Паколькі  ёсць бясконца малая паслядоўнасць, то лікавая паслядоўнасць  таксама (бмп), г.зн. . ■

def:Няхай –лікавая паслядоўнасць. Выраз выгляду , або

                                                             (1)

называецца лікавым шэрагам, а –яго –ым складнікам. Лік 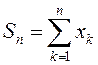 называецца -й частковай сумай шэрагу (1). Шэраг (1) называецца збежным , калі паслядоўнасць яго частковых сумаў  ёсць збежная. Калі паслядоўнасць  мае ліміт , то лік  называюць сумай шэрагу (1) і пішуць 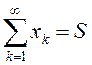. Калі паслядоўнасць  ёсць разбежная, то кажуць, што шэраг (1)–разбежны.

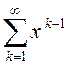Прыклад.Разгледзім лікавую паслядоўнасць  – бясконцую геаметрычную прагрэсію з назоўнікам . Разгледзім шэраг  , які выражае суму гэтай геметрычнай прагрэсіі, калі ён збежны. Гэты шэраг будзем называць геаметрычным. Паслядоўнасць яго частковых сумаў вызначаецца роўнасцю 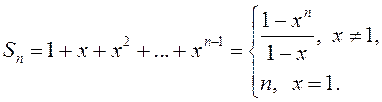 Паколькі лікавая паслядоўнасць  ёсць (бмп) толькі пры , то пры  мае месца  (Чаму? ), а пры  і  паслядоўнасць  ёсць разбежная (яна (бвп) ). Калі ж , то . Дакажам яе разбежнасць. Дапусцім яна мае . Пры  , г.зн. маюць месца няроўнасці . Далей маем  ?!?

Такім чынам, шэраг 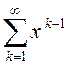 ёсць збежны толькі пры , і яго сума роўная , г.зн.

.

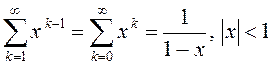Разгледзім асноўныя ўласцівасці збежных лікавых паслядоўнасцяў.

1º Збежная лікавая паслядоўнасць мае толькі адзін ліміт.

□ (ад процілеглага) Няхай лікавая паслядоўнасць  мае два ліміты  і . Паколькі , то , дзе  – бясконца малая паслядоўнасць. Такім жа чынам з , вынікае, што ,  – (бмп). Адсюль з роўнасці , атрымліваем, што . Паколькі  ёсць бясконца малая і сталая лікавая паслядоўнасць, то згодна ўласцівасці 4° (бмп) з §2.1 маем, што  , або .   ■

2º Збежная лікавая паслядоўнасць ёсць абмежаваная.

□ Няхай . Калі ўзяць , то знойдзецца лік  такі, што  праўдзіцца няроўнасць . У такім разе мае месца наступная няроўнасць . Калі выберам далей

, то атрымаем , г.зн. – абмежаваная лікавая паслядоўнасць. ■

Заўвага 3. Абмежаванасць лікавай паслядоўнасці ёсць умова неабходная, але не дастатковая для яе збежнасці. Напрыклад, лікавая паслядоўнасць    ёсць абмежаваная, але разбежная паслядоўнасць.

(Дакажыце яе разбежнасць)

(∆ Сапраўды, калі дапусціць процілеглае, што гэтая паслядоўнасць мае ліміт , то для  Але ж  набывае па чарзе значэнні  або  і таму маюць месца дзве няроўнасці . Улічваючы гэтыя няроўнасці, выканаем наступныя пераўтварэнні