Итак, зная инварианты и формулы
преобразования координат, можно вычислить полуоси эллипса и выяснить его расположение
относительно исходной системы координат  .
.
Пункт 2. Линии гиперболического типа (![]() ).
).
Справедливо следующее утверждение.
Теорема 3.2.2:Уравнение (*) линии L гиперболического типа при ![]() представляет
собой гиперболу, а при
представляет
собой гиперболу, а при ![]() —
пару пересекающихся прямых.
—
пару пересекающихся прямых.
Доказательство. Так как для уравнения (3.2.1) ![]() (т.к
(т.к ![]() ), то из условия
), то из условия
![]() вытекает, что ,
вытекает, что , ![]() и
и ![]() имеют разные знаки, Для определенности будем считать
имеют разные знаки, Для определенности будем считать ![]() ,
, ![]() (случай
(случай ![]() ,
, ![]() рассматривается
аналогично). Тогда уравнение (3.2.1) может быть записано следующим образом:
рассматривается
аналогично). Тогда уравнение (3.2.1) может быть записано следующим образом:
при ![]()
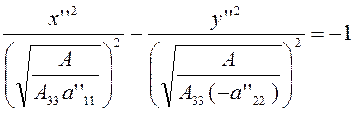 (3.2.5)
(3.2.5)
при ![]()
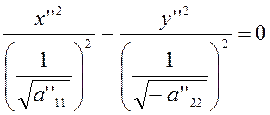 (3.2.6)
(3.2.6)
при ![]()
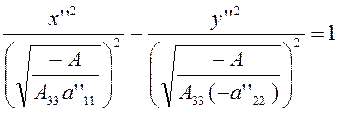 (3.2.7)
(3.2.7)
Очевидно, уравнение (3.2.5), отвечающее
случаю ![]() , представляет собой каноническое уравнение гиперболы, для
которой ось Оу является действительной осью, а ось Ох — мнимой
осью, причем мнимая и действительная полуоси этой гиперболы соответственно
, представляет собой каноническое уравнение гиперболы, для
которой ось Оу является действительной осью, а ось Ох — мнимой
осью, причем мнимая и действительная полуоси этой гиперболы соответственно 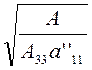 равны и
равны и 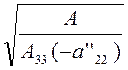 .
.
Уравнение (3.2.7), отвечающее случаю ![]() , также
представляет собой каноническое уравнение гиперболы, для которой ось Ох является
действительной осью, а ось Оу — мнимой осью, причем мнимая и
действительная полуоси этой гиперболы соответственно равны
, также
представляет собой каноническое уравнение гиперболы, для которой ось Ох является
действительной осью, а ось Оу — мнимой осью, причем мнимая и
действительная полуоси этой гиперболы соответственно равны 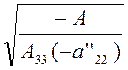 и
и 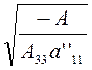 .Уравнение (3.2.6),
отвечающее случаю
.Уравнение (3.2.6),
отвечающее случаю ![]() ,
можно записать в виде
,
можно записать в виде
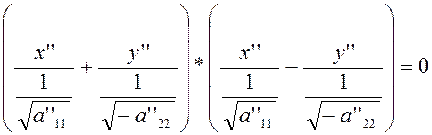
Этому последнему уравнению удовлетворяют лишь координаты точек, расположенных на прямых
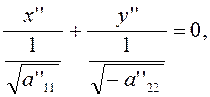
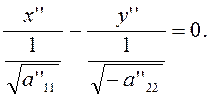
Для завершения доказательства теоремы
достаточно заметить, что каждое из уравнений (3.2.5) —(3.2.7) эквивалентно
исходному уравнению (*) соответственно для случаев ![]() ,
,
![]() ,
, ![]() , и поэтому
сделанные выше геометрические выводы для уравнений (3.2.5) — (3.2.7)
справедливы и для уравнения (*). Теорема доказана.
, и поэтому
сделанные выше геометрические выводы для уравнений (3.2.5) — (3.2.7)
справедливы и для уравнения (*). Теорема доказана.
Замечание 1. Остановимся подробнее на случае, когда
уравнение (*) гиперболического типа определяет гиперболу, т. е. когда ![]() .
.
Координаты (![]() )
центра этой гиперболы представляют собой решение системы (3.1.1). Угол наклона
)
центра этой гиперболы представляют собой решение системы (3.1.1). Угол наклона ![]() оси Ох' (являющейся
либо действительной, либо мнимой осью гиперболы) со старой осью Ох может
быть найден по формуле (3.1.6). Наконец, в
процессе доказательства теоремы были указаны величины действительной и мнимой
полуосей гиперболы. Их значения вычисляются через
оси Ох' (являющейся
либо действительной, либо мнимой осью гиперболы) со старой осью Ох может
быть найден по формуле (3.1.6). Наконец, в
процессе доказательства теоремы были указаны величины действительной и мнимой
полуосей гиперболы. Их значения вычисляются через ![]() ,
, ![]() ,
,![]() и
и ![]() . Коэффициенты
. Коэффициенты ![]() и
и ![]() выражаются
через коэффициенты
выражаются
через коэффициенты ![]() исходного уравнения (*) (см. первую и третью формулы (2.2.12); при этом
нужно положить
исходного уравнения (*) (см. первую и третью формулы (2.2.12); при этом
нужно положить ![]() и
и ![]() ). Уравнения асимптот
гиперболы без труда могут быть найдены по ее каноническим уравнениям (3.2.5)
или (3.2.7).
). Уравнения асимптот
гиперболы без труда могут быть найдены по ее каноническим уравнениям (3.2.5)
или (3.2.7).
Итак, зная инварианты и формулы
преобразования координат, можно вычислить действительную и мнимую полуоси гиперболы
и выяснить ее расположение относительно исходной системы координат 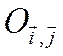 .
.
Параграф 3.
Упрощение уравнения линии параболического типа (![]() ). Классификация
линий параболического типа.
). Классификация
линий параболического типа.
Заметим, во-первых, что для
уравнения (*) параболического типа инвариант![]() отличен от нуля.
В самом деле, если
отличен от нуля.
В самом деле, если ![]() , то
, то ![]() , т.е.
, т.е. 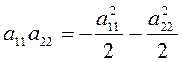 .
Так как
.
Так как ![]()
то, используя только что полученное
выражение для ![]() , найдем что
, найдем что 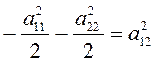 , откуда следует,
что
, откуда следует,
что ![]() . Но, по
предположению, по крайней мере один из коэффициентов
. Но, по
предположению, по крайней мере один из коэффициентов ![]() отличен от нуля. Итак,
отличен от нуля. Итак, ![]() .
.
Произведем стандартное упрощение уравнения (*):
1) если ![]() , то оставим
систему координат
, то оставим
систему координат 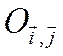 неизменной и изменим
лишь обозначение х на х', у на у',
неизменной и изменим
лишь обозначение х на х', у на у', ![]() на
на ![]() .
.
2) если ![]() , то перейдем к
повернутой системе координат
, то перейдем к
повернутой системе координат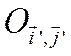 ,
вычисляя угол поворота по формуле (3.1.6)
и используя при этом формулы (2.2.12). В обоих указанных случаях уравнение (*)
примет вид (3.1.7). Так как для уравнения (3.1.7)
,
вычисляя угол поворота по формуле (3.1.6)
и используя при этом формулы (2.2.12). В обоих указанных случаях уравнение (*)
примет вид (3.1.7). Так как для уравнения (3.1.7) ![]() ,
, ![]() , то из условия
, то из условия ![]() вытекает, что
один из коэффициентов
вытекает, что
один из коэффициентов ![]() и
и ![]() равен нулю, а
другой не равен нулю.
равен нулю, а
другой не равен нулю.
Для определенности будем считать
![]() (случай
(случай
![]() рассматривается
аналогично). При этом предположении
рассматривается
аналогично). При этом предположении ![]() , так как
, так как ![]() Итак, уравнение линии (*) параболического типа после стандартного
упрощения может быть записано в следующей форме):
Итак, уравнение линии (*) параболического типа после стандартного
упрощения может быть записано в следующей форме):
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.