Инварианты кривых второго порядка и их канонические уравнения. Канонические уравнения, страница 4

Если мы имеем преобразование общего вида (перенос начала, сопровождаемый изменением координатных векторов), то значения новых коэффициентов получим по предыдущим формулам, произведя последовательно перенос начала, а затем изменение координатных векторов (или в обратном порядке).

До сих пор речь шла о преобразовании полинома F (х, у) при изменении системы координат.

Если речь идет об уравнении данной линии F (х, у) = 0, то уравнение той же линии в новой системе 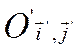 мы можем получить, заменяя в полиноме

F (х, у) переменные х, у их выражениями через х', у'. Но после этого мы можем еще умножить полученное таким образом уравнение

на произвольный постоянный множитель k, отличный от нуля. Тогда коэффициенты нового уравнения не будут уже теми, которые определяются предыдущими формулами, однако будут отличаться от них только постоянным множителем (притом произвольным, но отличным от нуля).

Когда в дальнейшем будет идти речь о преобразовании уравнения линии при замене координат, мы будем всегда подразумевать (если противное не оговорено особо), что преобразование производится без умножения на постоянный множитель, т. е. что речь идет о преобразовании полинома

F (х, у).

Параграф 3. Понятие инварианта. Примеры.

При переходе от одной декартовой системы координат к другой коэффициенты уравнения линий, конечно, изменяются, однако каждое данное уравнение линии определяет не только её расположение относительно выбранной системы координат, но и её внутренние свойства, не зависящие от системы координат.

Поэтому должны существовать такие функции коэффициентов, которые сохраняют свои значения в любой декартовой системе координат («инварианты уравнения линии»).

Если сложим первые две формулы (2.2.12), то получим

Значит, хотя при повороте осей координат величины и  изменяются каждая в отдельности (обращаются в новые величины  и ), но сумма их остается неизменной. Также и  остаются неизменными при переносе начала. Итак, сумма коэффициентов при квадратах переменных

                (2.3.13)

остается неизменной при любом преобразовании прямоугольных координат. Это обстоятельство выражают, говоря, что  S есть инвариант полинома

F (х, у) при преобразовании прямоугольных координат.

Вообще, всякая функция

от коэффициентов полинома F (х, у) называется инвариантом при преобразовании прямоугольных координат, если значение этой функции остается неизменным при переходе от данной прямоугольной системы к любой другой прямоугольной, т. е. если

.

Основное значение понятия инварианта станет ясным, если заметить, что выражение вида только в том случае может представлять геометрическую величину, характерную для самой рассматриваемой линии, а не зависящую от случайного положения осей координат, если это выражение есть инвариант. Поэтому вопрос о разыскании инвариантов полинома F (х, у) является одним из самых основных в теории линий второго порядка.

Будем  разыскивать инварианты при преобразовании прямоугольных координат, или, как говорят, ортогональные инварианты; в дальнейшем, говоря об инвариантах, мы будем подразумевать ортогональные инварианты, если противное не оговорено особо.

Приведем еще один пример инварианта. Формулы (2.2.12)  дают

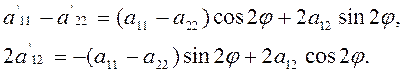
Возведем эти равенства в квадрат

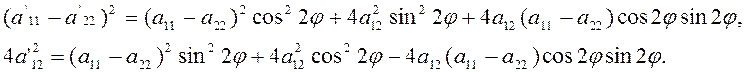
и сложим, получим

.

Следовательно, выражение

         (2.3.14)

есть также инвариант.

Оно может быть переписано еще так:

.

Если мы имеем несколько инвариантов     , то всякая их функция  будет также инвариантом. Это совершенно ясно, так как если  остаются неизменными при замене координат, то и  останется неизменной.

Таким образом, например,   есть инвариант, ибо

S есть инвариант. Вычитая  из только что найденного инварианта , получим инвариант , или, отбросив постоянный множитель - 4, инвариант

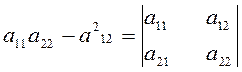. (2.3.15)

Параграф 4. Основные инварианты уравнения линии второго

порядка.