Инварианты кривых второго порядка и их канонические уравнения. Канонические уравнения, страница 6

, . (По теореме Виета и следствию из неё)

К инвариантам могут быть также причислены ранги определителей А и .

Параграф 5. Метрические   инварианты  в случае обобщенных декартовых координат

Формулы, выражающие метрические свойства линии второго порядка, не должны зависеть от положения линии по отношению к системе декартовых координат, но они, вообще говоря, зависят от длин координатных векторов u, v и угла  между ними (т. е. от формы и размеров системы, но не от ее положения относительно линии).

Форма и размеры системы вполне характеризуются коэффициентами квадратичной формы (которую мы будем называть основной метрической формой)

, (2.5.1)

выражающей квадрат длины произвольного вектора Р (X, Y).  В основной метрической форме:

                 (2.5.2)

что вполне определяет ,и когда даны .( они должны быть всегда задаваемы так, чтобы форма (1) была положительной. Это выполняется если )

В соответствии с этим, под метрическими инвариантами полинома F (х, у) мы будем понимать функции

, зависящие от коэффициентов полинома Fи от коэффициентов основной метрической формы (2.5.1), остающиеся неизменными при замене данной декартовой системы произвольной другой декартовой системой.

Мы найдем метрические инварианты, обобщающие ортогональные инварианты  А,  , S и сводящиеся к этим последним в случае прямоугольной системы (т. е. когда  ).

Заметим с этой целью следующее. При подстановке

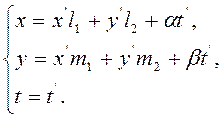 (2.5.3)

форма переходит в форму ; дискриминанты А и  этих форм связаны соотношением

,         (2.5.4)

где

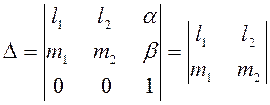.            (2.5.5)

Подстановке (2.5.3) соответствует следующая подстановка для координат вектора:

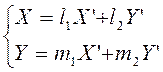          (2.5.3а)

при этой подстановке форма (1) обращается в форму

.               (2.5.)

Дискриминант

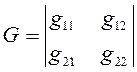      (2.5.6)

формы (2.5.1) связан с дискриминантом  формы (2.5.) соотношением

               (2.5.7)

где  – тот же самый определитель, что и в (4), как это видно на основании

(2.5.5). Из (2.5.4) и (2.5.7) следует

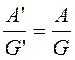, т. е.    есть метрический инвариант.

Точно так же докажем, что    где   обозначает  по-прежнему дискриминант формы

, есть инвариант при преобразованиях, не изменяющих начала системы координат. Рассмотрим, наконец, форму

На основании сказанного выше, отношение дискриминанта этой формы к G, т. е. отношение

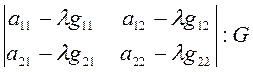
есть инвариант при замене системы координат без изменения начала. Раскроем определитель:

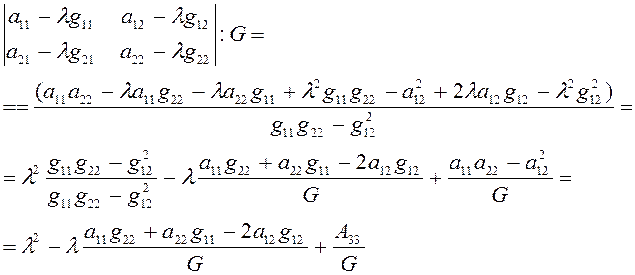
Так как последнее выражение инвариантно при всяких , то все коэффициенты при различных степенях — инварианты. Свободный член и коэффициенты при  не дают ничего нового. Остается еще один новый инвариант:

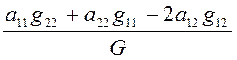
Итак, мы нашли три инварианта:

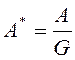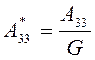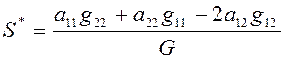,  ,    (2.5.8)

Инвариантность последних двух выражений доказана пока только при условии неизменности начала; но, очевидно, перенос начала вовсе не влияет на     и  ; что же касается до  то при их преобразовании мы пользуемся формулами (3а) для координат вектора, где положение начала вовсе не играет никакой роли.

В случае необобщенной декартовой (косоугольной) системы

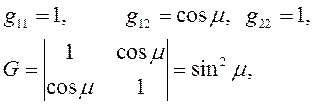
и инварианты (8) принимают вид

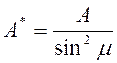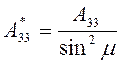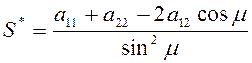,  ,       (2.5.9)

При 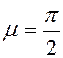эти   инварианты  обращаются в ортогональные инварианты А,

, S.

Глава 3. Классификация линий второго порядка.

Геометрические характеристики линии второго порядка и их расположение вполне определяются значениями инвариантов S, A, . В зависимости от знака инварианта   эти линии разделяют на следующие три типа:

эллиптический тип, если  > 0,

гиперболический тип, если < 0,

параболический тип, если  = 0.

Очевидно, тип линии не меняется при изменении декартовой системы координат. Ниже будет приведена полная классификацию каждого из указанных типов линий.

Параграф 1. Основные определения. Стандартные упрощения.

Пункт 1. Центр линии второго порядка.

Ранее было установлено, что при параллельном переносе системы координат изменяются лишь коэффициенты группы линейных членов уравнения линии второго порядка.