Пусть дана квадратичная форма
![]() (2.1.20)
(2.1.20)
и пусть вместо переменных ![]() введены новые переменные
введены новые переменные ![]() при помощи линейной подстановки
при помощи линейной подстановки
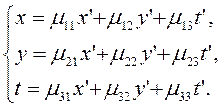 (21)
(21)
Тогда форма ![]() превратится в квадратичную форму
превратится в квадратичную форму ![]()
Параграф 2. Преобразование уравнения при замене декартовых координат.
Выясним, как изменяются коэффициенты левой части
![]() (2.2.1)
(2.2.1)
уравнения линии второго порядка при замене
данной системы декартовых координат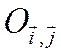 другою
другою 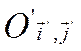 .
.
Мы знаем, что при такой замене старые и новые координаты одной и той же точки связаны линейными соотношениями вида
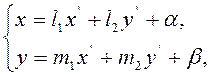 (2.2.2)
(2.2.2)
где постоянные ![]() зависят от положения новой системы относительно старой и от
размеров и направлений координатных векторов. А именно,
зависят от положения новой системы относительно старой и от
размеров и направлений координатных векторов. А именно, ![]() обозначают координаты
нового начала
обозначают координаты
нового начала ![]() относительно
старой системы, а
относительно
старой системы, а ![]() и
и
![]() — координаты новых координатных векторов. В частности, в
случае, когда обе системы — прямоугольные, одного и того же класса, причем
новая система получается из старой путем переноса начала в точку (
— координаты новых координатных векторов. В частности, в
случае, когда обе системы — прямоугольные, одного и того же класса, причем
новая система получается из старой путем переноса начала в точку (![]() ) и поворота на
угол
) и поворота на
угол ![]() , формулы (2.2.2)
принимают вид
, формулы (2.2.2)
принимают вид
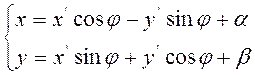 (2.2.3)
(2.2.3)
Если внести в полином (2.2.1) вместо х,
у их выражения (2.2.2), то ![]() обратится в полином также второй степени относительно х',
у'. Этот полином мы обозначим через
обратится в полином также второй степени относительно х',
у'. Этот полином мы обозначим через ![]() , а коэффициенты его —
соответственно через
, а коэффициенты его —
соответственно через ![]() и т. д., так что
и т. д., так что
![]() . (2.2.4)
. (2.2.4)
Новые коэффициенты ![]() будут, конечно,
определенным образом зависеть от старых коэффициентов
будут, конечно,
определенным образом зависеть от старых коэффициентов ![]() и от коэффициентов формул преобразования (2.2.2). Вопрос о
выражении новых коэффициентов через старые, для упрощения выкладок, разобьем
на два, рассматривая отдельно случай переноса начала координат без изменения
координатных векторов и случай изменения координатных векторов без изменения
начала.
и от коэффициентов формул преобразования (2.2.2). Вопрос о
выражении новых коэффициентов через старые, для упрощения выкладок, разобьем
на два, рассматривая отдельно случай переноса начала координат без изменения
координатных векторов и случай изменения координатных векторов без изменения
начала.
Пункт 1. Перенос начала.
В этом случае, если начало перенести в
точку О' (![]() ), старые координаты (х, у) связаны с новыми
координатами (х', у') уравнениями
), старые координаты (х, у) связаны с новыми
координатами (х', у') уравнениями
![]() ,
, ![]() .
(2.2.5)
.
(2.2.5)
Подставляя эти значения в полином (2.2.1) и пользуясь формулой (2.1.17 а), получим
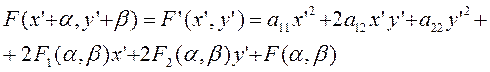 (2.2.6)
(2.2.6)
итак, получили следующий простой результат :
При переносе начала координат в точку (![]() ) полином F (х, у) преобразуется следующим образом:
коэффициенты членов второго измерения остаются без изменения. Коэффициенты при
первых степенях новых переменных х' и у' равны соответственно значениям частных
производных
) полином F (х, у) преобразуется следующим образом:
коэффициенты членов второго измерения остаются без изменения. Коэффициенты при
первых степенях новых переменных х' и у' равны соответственно значениям частных
производных ![]() ,
, ![]() полинома F (х, у) в точке (
полинома F (х, у) в точке (![]() ); наконец,
свободный член равен значению полинома F (х, у) в той же точке (
); наконец,
свободный член равен значению полинома F (х, у) в той же точке (![]() ).
).
Получаем:
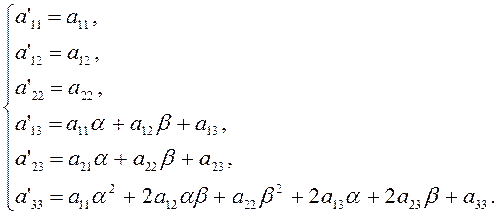 (2.2.6а)
(2.2.6а)
Пункт 2.Изменение координатных векторов без изменения начала.
В этом случае
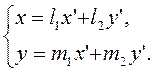 (2.2.7)
(2.2.7)
Если подставить эти выражения в полином F (х, у), то мы получим полином F' (х’, у'). Совершенно очевидно, на основании однородности формул преобразования (2.2.7), что члены второго измерения в полиноме F' (х', у') произойдут исключительно от членов второго измерения в F (х, у), члены первого измерения — от членов первого измерения, и что член нулевого измерения (свободный член) не изменится вовсе.
Таким образом, будем иметь
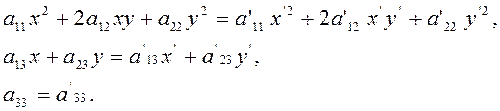 (2.2.8)
(2.2.8)
(2.2.9)
Чтобы получить выражения новых коэффициентов при членах второго измерения, достаточно воспользоваться равенством (2.2.8), которое должно обратиться в тождество, если в левую часть вместо х, у внести их выражения (2.2.7). Это даст
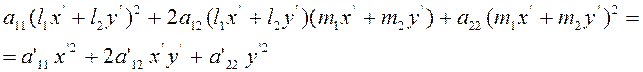
Раскроем скобки в левой части
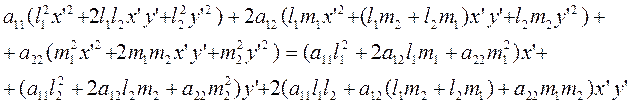
и приравняем коэффициенты при ![]() в обеих частях,
получим
в обеих частях,
получим
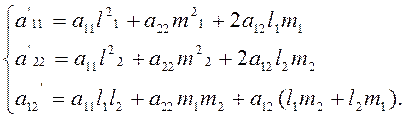 (2.2.10)
(2.2.10)
Точно так же получим выражения новых коэффициентов при членах первого измерения, при помощи формулы (2.2.9), которая дает
![]() , откуда (сравнивая коэффициенты):
, откуда (сравнивая коэффициенты):
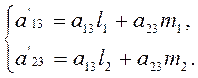 (2.2.11)
(2.2.11)
И, наконец
![]()
В случае поворота осей прямоугольных координат, когда формулы преобразования имеют вид
![]()
т. е. когда
![]() , предыдущие формулы дают
, предыдущие формулы дают
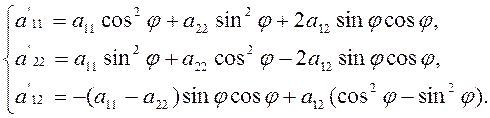 (2.2.10а)
(2.2.10а)
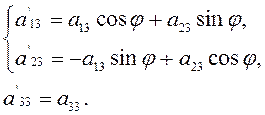 (2.2.11а)
(2.2.11а)
Формулы (2.2.10а) можно несколько упростить. Именно, вспоминая, что
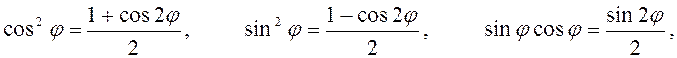
получим формулы:
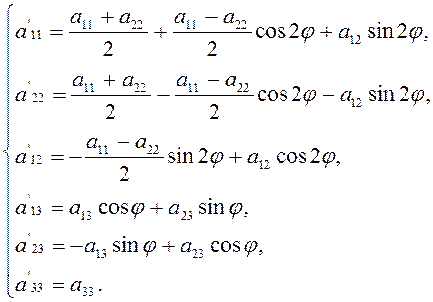 (2.2.12)
(2.2.12)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.