Инварианты кривых второго порядка и их канонические уравнения. Канонические уравнения, страница 5

Инварианты, найденные в предыдущем параграфе, могут быть получены еще иным путем на основании свойства дискриминанта квадратичной формы: дискриминант преобразованной формы равен дискриминанту исходной формы, умноженному на квадрат определителя подстановки; этим же путем мы найдем еще один инвариант и получим, таким образом, все основные ортогональные инварианты, связанные с уравнением линии второго порядка.

Рассмотрим с этой целью квадратичную форму

         (2.4.1)

получающуюся из полинома F (х, у) «дополнением до однородности», а также квадратичную форму

,                      (2.4.2)

представляющую собою совокупность членов второго измерения полинома

F (х, у).

Известно, что дискриминант квадратичной формы (2.4.1) есть 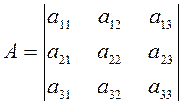, и что дискриминант квадратичной формы (2.4.2) представляет собою алгебраическое дополнение  элемента а₃₃ в предыдущем определителе:

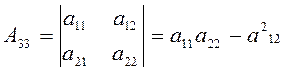 ,              (2.4.3)

Вспомним теперь предложение, гласящее, что дискриминант квадратичной формы, получающейся из данной в результате линейной однородной подстановки над переменными, равен дискриминанту исходной формы, умноженному на квадрат определителя подстановки.

При переходе от системы прямоугольных осей 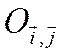 к системе прямоугольных осей 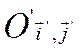переменные х, у в полиноме F (х, у) подвергаются неоднородной подстановке. (Если  системы координат — разного класс, то вместо формул (2..4.4) будем иметь формулы

         )

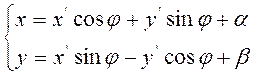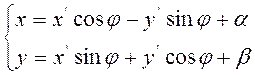               (2.4.4)

Чтобы иметь дело с линейной однородной подстановкой над переменными х, у, tквадратичной формы , будем подвергать эти переменными  подстановке

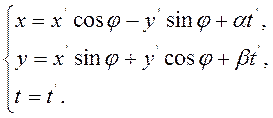          (2.4.4а)

При    эта подстановка обращается в подстановку (2.4.4), а исходная и преобразованная формы и

обращаются в исходный и преобразованный полиномы F (х, у) и F' (х', у').

Определитель подстановки (2.4.4а) равен

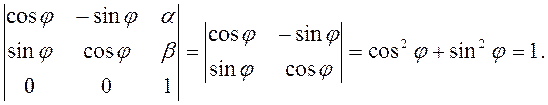
Поэтому дискриминант А квадратичной формы  останется неизменным при замене координат, т. е. мы будем иметь

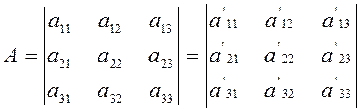
Итак, дискриминант А есть инвариант.

Применим теперь ту же теорему к квадратичной форме , рассматривая линейную подстановку

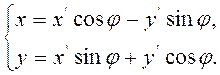             (2.4.5)

Так как определитель этой подстановки равен 1, то дискриминант квадратичной формы

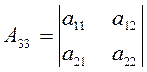
остается неизменным при повороте осей координат. Так как, далее, перенос начала вовсе не изменяет коэффициентов  полинома , то  остается неизменным при всяком преобразовании прямоугольных координат. Таким образом, инвариантность  доказана снова.

Рассмотрим, далее, квадратичную форму

 

   (*)

где — произвольная постоянная.

При подстановке (2.4.5) эта квадратичная форма переходит в форму

  (**)

ибо при подстановке (2.4.5) имеем тождественно

.

Так как дискриминанты форм (*) и (**) должны быть равны между собою, то

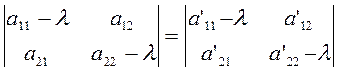, или, раскрывая определители:

.

Это соотношение должно иметь место при всяких , следовательно, коэффициенты при различных степенях , должны быть одинаковы в правой и левой частях. Это дает

 .

Второе из этих равенств выражает инвариантность ; первое же показывает, что

есть также инвариант — результат, полученный в предыдущем параграфе иным путем.

Итак, мы приходим к следующему важному выводу: выражения

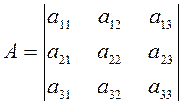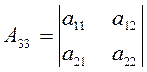, ,   (2.4.6)

 ортогональные инварианты полинома F (х, у).

и   соответственно дискриминанты форм  и . Мы будем их, для краткости, называть соответственно

«большим» и «малым» дискриминантами полинома F (х, у).

Замечание:  Кроме инвариантов (2.4.6) можно составить бесчисленное множество других: всякая функция от А,  , Sбудет также инвариантом. Вопрос о том, является ли, обратно, всякий инвариант функцией указанных трёх, будет рассмотрен ниже .

Отметим, что, в частности, корни   и квадратного уравнения

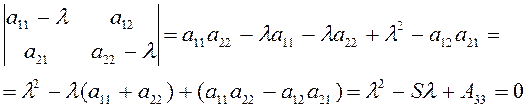,   (2.4.7)

также  являются инвариантами, ибо коэффициенты этого уравнения не изменяются при замене прямоугольных координат. В противоположность инвариантам (2.4.6) величины—  и  иррациональные инварианты (т. е. не выражаются рационально через коэффициенты полинома F). Инварианты S и  являются  функциями от  и :