Еще одной характерной разницей между МКЭ и МКР является то, что по своей сути МКЭ приспособлен для решения задач с наличием существенно влияющих границ, а МКР в основе своей предполагает наличие некоторой непрерывной (в идеале неограниченной) среды в которой и проводиться поиск распределения некоторой функции. В такой среде действительно становится неважным жесткая ортогональность граней разностной ячейки. В непрерывной среде любой поток можно абсолютно адекватно описать тремя ортогональными составляющими и совершенно произвольно назначить расположение границ расчетной ячейки, в том числе и ортогонально, как это происходит в МКР. При этом следует понимать, что «непрерывность» среды не означает одинаковость свойств этой среды, она лишь означает, что искомое распределение не прерывается на некоторых границах. Однако, в общем случае ЛП как раз и предполагают наличие таких границ – в первую очередь между отливкой и формой. В связи с этим можно показать, что МКР всегда дает ПРИНЦИПИАЛЬНО НЕПРАВИЛЬНОЕ решение для граничных задач при наличии произвольно расположенных границ. Хотя, следует отметить, что вопрос о величине погрешности МКР при наличии границ зависит от того, насколько велики потоки через эти границы, а в конечном итоге от того, насколько велик разрыв функции на границе. Известно, что применительно к ЛП, этот разрыв относительно невелик при малотеплопроводных формах (литье в песчаные формы) и относительно велик при высокотеплопроводных формах (литье в кокиль). (Конкретные значения таких ошибок рассмотрим ниже.)
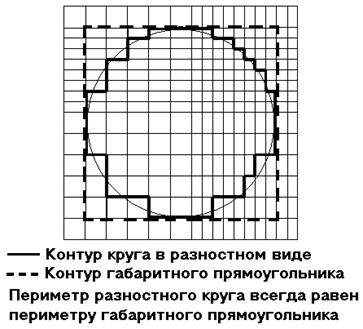
Рис.3 Пример двумерной сетки МКР и ошибки при определении периметра,
которая не зависит от густоты разностной сетки.
При наличии граничных потоков всегда становится существенным соблюдение соотношения между объемом и площадью границ. Например, такая широко известная в литье характеристика, как «приведенная толщина», которая определяет время затвердевания, является отношением объема к теплоотводящей поверхности. Очевидно, что в МКЭ увеличивая дискретность сетки можно сколь угодно точно приблизиться как к реальному значению объема моделируемой геометрии, так и к реальному значению внешней площади этой геометрии. В отношении же МКР это справедливо только по отношению к объему. Все более и более измельчая сетку, в МКР можно все больше приближаться к истинной величине объема. (Хотя, как было показано выше, с гораздо меньшей точностью, чем при МКЭ.) Однако, как это не неожиданно, величина площади внешней поверхности геометрии в разностном представлении практически не будет зависеть от густоты сетки и всегда будет одинаково неправильной при любой, сколь угодно мелкой дискретизации. Чтобы пояснить это, рассмотрим (см. рис.3) двумерный случай разностной разбивки круга. На рис.3 видно, что поскольку все границы круга описаны либо вертикальными, либо горизонтальными отрезками, то периметр этой фигуры всегда будет равен периметру квадрата, в который вписан этот круг, т.е. периметр разностного «круга» равен четырем диаметрам. При этом от шага сетки этот результат совершенно не зависит. В действительности же, периметр круга, как известно равен произведению числа «пи» на диаметр. Для примера можно вычислить ошибку, которую даст разностный метод при определении времени затвердевания неограниченного цилиндра в среде с постоянной температурой. Как известно, время затвердевания такого цилиндра будет пропорционально квадрату приведенной толщины [6]. Тогда, предполагая, что дискретность достаточна для точного вычисления поперечной площади цилиндра и делая очевидные преобразования, можно вычислить ошибку МКР в процентах от реального времени затвердевания:
Δτ = ( 1-(π/4)2 )*100%=38%. (1)
Таким образом, при использовании МКР время затвердевания цилиндра будет на 38% меньше, чем реальное. Следует подчеркнуть, что вычисленная погрешность МКР - это не ошибка численного решения или недостаточной дискретизации, а постоянная погрешность разностного метода для цилиндрических конфигураций. Для шара она будет больше, а для плиты ориентированной параллельно одной из плоскостей разностной разбивки отсутствует вовсе. Очевидно, что при тех же условиях ошибка для МКЭ будет нулевой для всех конфигураций.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.