Свойства кристаллических твёрдых тел. Колебания частиц в кристаллической решетке. Уравнение состояния твердого тела. Электронная подсистема твердого тела, страница 6

элементы симметрии решетки. Этот метод состоит в следующем. Из какого-либо центра, совпадающего с одним из атомов (узлом решетки), проводятся прямые, соединяющие данный атом с ближайшими соседями. Далее через середину этих прямых проводятся плоскости, перпендикулярные к ним. Такая совокупность плоскостей выделяет вблизи данного атома некоторый объем. Он носит название ячейки Вигнера—Зейтца. (E.P. Wigner, F. Seitz).Пример построения такой ячейки для плоской решетки показан на рис. 1.8. Важно отметить, что объем ячейки Вигнера—Зейтца совпадает с объемом элементарной ячейки. Ячейка Вигнера—Зейтца по своему определению содержит атом в центре и сохраняет симметрию кристалла не только относительно трансляций, но и относительно всех других типов симметрии (например, поворотов и отражении (подробнее см. [1, 2, 4, 5, 10])).

1.2.2. Обратная решетка

Все характеристики кристаллов, включая распределения плотностей вещества и заряда в решетке, потенциальная энергия электронов в поле ионов и т. д., обладают, той или иной пространственной периодичностью. Если  — произвольная функция, зависящая от свойств кристалла, то в соответствии с определением периодической функции, она обладает свойством

                                                              (1.2)

где — вектор трансляции (1.1). Поскольку , как правило, достаточно гладкая функция, ее можно разложить в тройной ряд Фурье

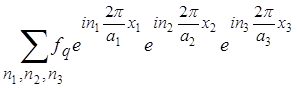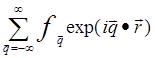==,                          (1.3)

где  — волновой вектор с компонентами q_j = 2πn_j/a_j, j = 1,2,3, имеющий размерность обратной длины. В этом случае  пробегает все узлы обратной решетки. Таким образом суммирование в (1.3) производится либо по всем , либо соответственно дискретному набору n₁, n_2, n₃.

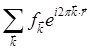=,                                      (1.4)

где вектор  — волновой вектор с компонентами k_j = n_j/a_j, j = 1,2,3, имеющий размерность обратной длины.

Если вспомнить, что , то

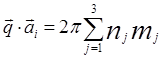 = 2πm,                                     (1.5)

где n_j, m_j целые числа, а, следовательно, и  m — целое число.

Легко проверить выполнения условие периодичности (1.2) для представлений (1.3), (1.4)

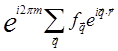====.                          (1.5)

Поскольку (1.5) справедливо для любого , всегда имеет место равенство

=1,                                                                 (1.6)

Отметим еще одно важное свойство периодических функций, представляемых рядом Фурье (1.3)

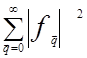f(r)²dr =,                                          (1.7)

Согласно (1.7), можно ввести вектор некоторый вектор трансляции в так называемой обратной решетке. и построить векторах обратной решетки

                                     = ,                                                          (1.8)

выбирая m_j, — целое число, j = 1,2.3.

Между базисными векторами прямой и обратной решеток можно установить взаимно однозначное соответствие, если определить  как

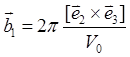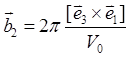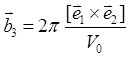, ,                     (1.9)

где =2πδ_ij, V₀ = — объем элементарной ячейки в прямой решетке; δ_ij — символ Кронекера.

Таким образом, с каждой решеткой Бравэ связана решетка в «обратном» пространстве. Очевидно, что в обратной решетке, так же, как и в кристаллической решетке, на основных векторах можно построить элементарные ячейки, включая и ячейку Вигнера—Зейтца. Различные(поставить перед элементарными ячейками?) Элементарной ячейке Вигнера—Зейтца в обратной решетке соответствет зона Бриллюэна (L. Brillouin). Из дальнейшего будет видно, что это понятие играет большое значение при расчете характеристик твердых кристаллических тел). Отметим некоторые свойства элементарной ячейки в обратной решетке:

а)  объём элементарной ячейки обратной решетки равен с точностью до множителя обратному объёму прямой решетки, т.е. ;

б) простые решетки всех систем решеток Бравэ имеют обратные также простые решетки;

в) объемно – центрированной решетке Бравэ соответствует гранецентрированная обратная решетка и т.д.;

г) векторы обратной решетки можно использовать для маркировки атомных плоскостей прямой решетки.

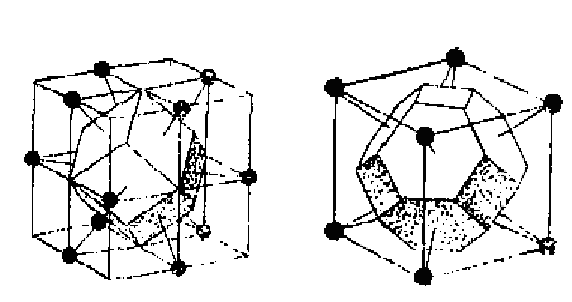
Рис. 1.9.а                                         Рис. 1.9.б