Свойства кристаллических твёрдых тел. Колебания частиц в кристаллической решетке. Уравнение состояния твердого тела. Электронная подсистема твердого тела, страница 30

Можно показать, что является периодической функцией с периодом решетки, т.е. . Действительно:

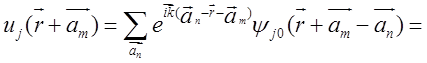
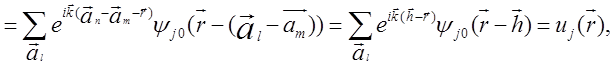
где  .

Введем нормировку функции  на полное число частиц в кристалле

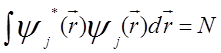.                                 (5.85)

Здесь N – число частиц в кристалле. Запишем уравнение Шредингера

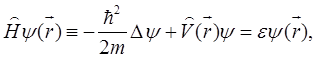                                    (5.86)

где  – эффективный потенциал всей решетки. Запишем энергию электрона в кристалле в состоянии . Для этого умножим (5.85) слева на  и, проинтегрировав по объему, получим:

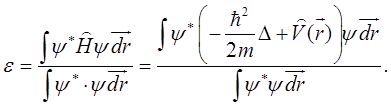                                                   (5.87)

Левую часть уравнения Шредингера (5.86) можно записать в виде 

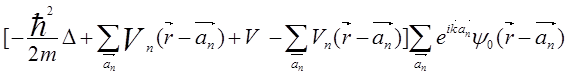, добавляя и вычитая функцию 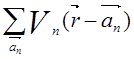,  где   - потенциал отдельного атома, находящегося в точке . Далее учтем, что невозмущенный оператор Гамильтона точных локализованных состояний есть

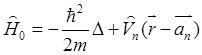 и .                  (5.88)

С учетом выше сказанного преобразуем выражение, стоящее в числителе дроби (5.87) может быть преобразовано к виду

=

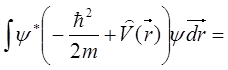
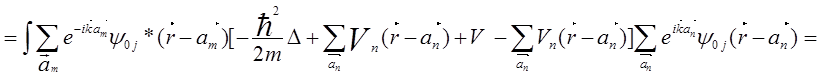
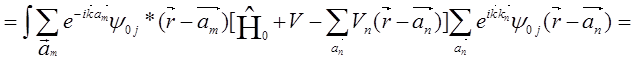
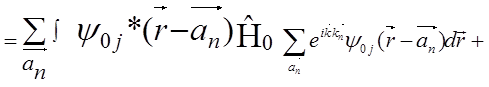
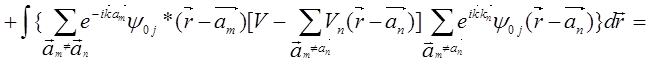
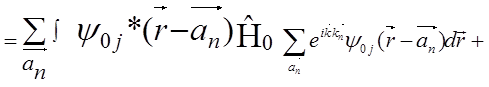
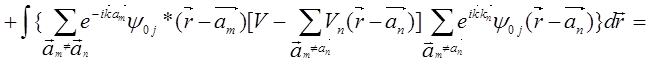
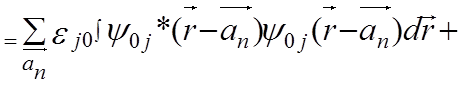
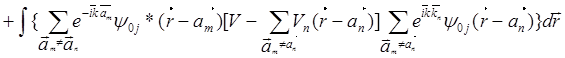=N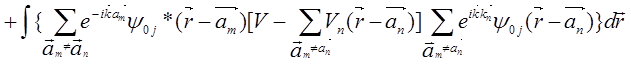.(5.89)

Преобразуем теперь второе слагаемое в формуле (5.87)

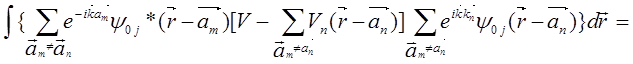
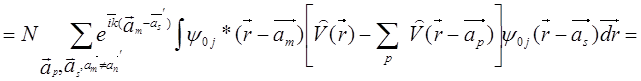
=N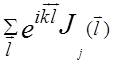,                                                            (5.90)

где

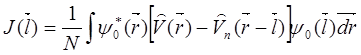                       (5.91)

При преобразовании вышеприведенного выражения учитывалось то, что вклад дают лишь области интегрирования, где каждая из двух, входящих в интеграл (5.91) функций f₁(r), f₂(r),

f₁(r)=  и f₂(r) =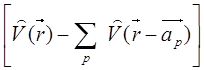                         (5.92)

отлична от нуля. Также учитывается, что из-за периодичности решетки интегралы в (5.5.88) зависят лишь от разности .

В результате изменение энергии дискретного уровня  (формула (5.87) с учетом (5.89) и (5.90)) теперь запишется в виде

   =       

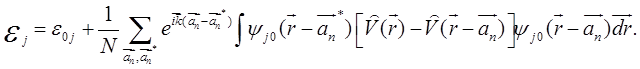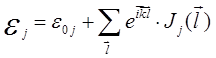                                                    (5.92)

где  — собственное значение энергии не возмущенного k-ого уровня, получаемое из решения уравнения Шрёдингера (5.88)

Введенная формулой (5.90) функция  носит название интеграла перекрытия. На рисунке 5.11 показано поведение функций f₁(r), f₂ (r) и f₃(r) = f₁(r) f₂(r) от одной из координат – r.

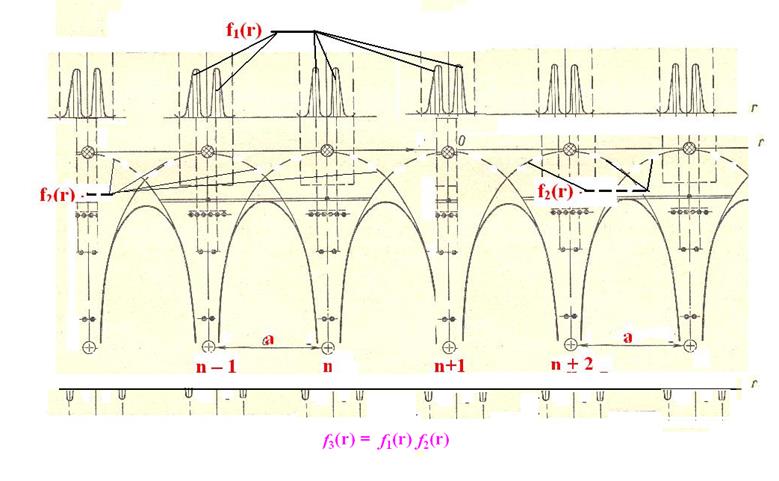
Рис. 5.11

Интеграл перекрытия, в подынтегральное выражение которого входят волновые функция, относящиеся к различным узлам решетки, весьма быстро убывает с ростом . Это нетрудно понять из физического смысла ,  так как он представляет собой вероятность перехода между состояниями и под действием потенциала . Подобные интегралы перекрытия встречаются в задачах расчета химической связи (например, для объяснения связи в молекуле водорода или воды)

В ряде случаев можно записать соотношение (5.92) в явном виде. Так, для одномерного случая в приближении ближайших соседей ; следовательно:

.                  (5.93)

В трехмерном случае для простой кубической решетки в приближении ближайших соседей (см. рис. 5.12a).

    

                                                 (5.94)

где  — модуль вектора трансляции решетки.

Таким образом, из полученных, соотношений видно, что при образовании кристалла из изолированных атомов энергия электрона при переходе от отдельного атома к кристаллу расщепляется в зону (в силу интеграла перекрытия), в пределах которой энергия электрона периодически зависит от волнового вектора . В этом случае картина качественно напоминает ту, которая была получена в приближении слабой связи. Однако в силу малости интеграла перекрытия (атомные волновые функции спадают с расстоянием очень быстро) имеет место неравенство

                        (5.95)

где — расстояние между энергетическими уровнями в изолированном атоме. С другой стороны, (5.95) дает ширину образовавшейся за счет взаимодействия электронов с ионами решетки зоны разрешенных состояний. Следовательно, в отличие от приближения слабой связи здесь зоны разрешенных состояний узкие, а зоны запрещенных состояний — широкие.

Проиллюстрируем теперь свойства электрона в решетке в приближении сильной связи. Рассмотрим при  и  :

          (5.96)

          (5.97)

где — величина, равная . Поскольку имеет место неравенство  (J~10^-19 эВ), то т_* > т. Таким образом, электрон внутри зоны Бриллюэна в окрестности точки k=0 можно трактовать как тяжелую частицу отрицательной эффективной массы , а в окрестности точки — как тяжелую частицу положительной эффективной массы т_* >> т.