Поскольку для существования
нетривиального решения определитель системы должен быть равен нулю, находим
собственные значения Гамильтониана ![]()
D(ε) = det![]() =
0. (5.46)
=
0. (5.46)
Если оставить в сумме (5.42) всего
два члена, то матрица оператора![]() вектор- столбец,
вектор- столбец, ![]() и определитель D(ε) выглядят
так
и определитель D(ε) выглядят
так
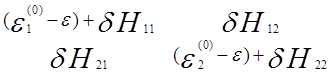 ,
,![]() ,
,
D(ε) = ![]() .
.
С учетом малого параметра δ при решении уравнений можно разлагать неизвестные величины в ряды по малому параметру
![]() ,
, ![]() , (5.47)
, (5.47)
Более подробно реализацию метода
теории возмущения рассмотрим для случая, когда в
невозмущенном состоянии электроны являются свободными, а в качестве возмущения
выступает оператор потенциальной энергии решетки ![]() =
= ![]() , который считается малым.
, который считается малым.
5.3.2. Энергетический спектр электронов с учетом взаимодействия с ионами (не вырожденный случай слабой связи)
В невозмущенном состоянии электроны
являются свободными, их волновая функция имеет
вид плоской волны ![]() ,
,
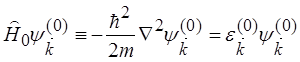 .
(5.48)
.
(5.48)
Энергетический спектр электронов
непрерывен ![]() . Попытаемся
применить стационарную теорию возмущений для вычисления энергетической
поправки к энергии свободного электрона. Из-за того, что энергетический спектр
электронов непрерывен, волновую функцию Гамильтониана
. Попытаемся
применить стационарную теорию возмущений для вычисления энергетической
поправки к энергии свободного электрона. Из-за того, что энергетический спектр
электронов непрерывен, волновую функцию Гамильтониана ![]() невозможно представить в
виде разложения по плоским волнам. В этом случае волновая функция может быть
представлена в виде интеграла Фурье
невозможно представить в
виде разложения по плоским волнам. В этом случае волновая функция может быть
представлена в виде интеграла Фурье
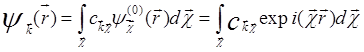 . (5.49)
. (5.49)
Подставляя (5.49) в возмущенное уравнение Шредингера, получим
(![]() )
)![]() =
=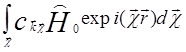 +
+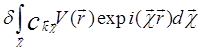 =
=
=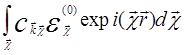 +
+ 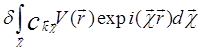 =
=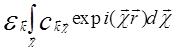 . (5.50)
. (5.50)
Учитывая, что оператор потенциальной энергии взаимодействия электронов с решеткой ![]() является периодической функцией
с периодом решетки, его можно представить в виде ряда Фурье
является периодической функцией
с периодом решетки, его можно представить в виде ряда Фурье
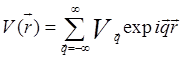 (5.51)
(5.51)
В итоге уравнение (5.50) можно записать в виде
(![]() )
)![]() =
=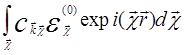 +
+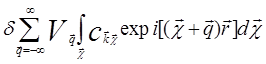 =
=
=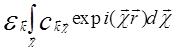 (5.52)
(5.52)
Далее нам понадобится еще одно свойство интегралов от плоских волн
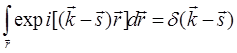 ,
(5.53)
,
(5.53)
где ![]() - дельта функция Дирака. Это свойство аналогично
свойству ортогональности дискретных собственных функций невозмущенного
оператора Гамильтона (5.44) .
- дельта функция Дирака. Это свойство аналогично
свойству ортогональности дискретных собственных функций невозмущенного
оператора Гамильтона (5.44) .
Умножим уравнение Шредингера (5.52)
на ![]() и проинтегрируем по
объему кристалла
и проинтегрируем по
объему кристалла
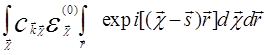 +
+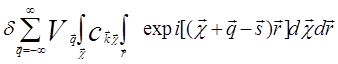 =
=
=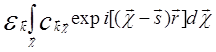 .
(5.54)
.
(5.54)
Поменяем теперь в (5.54) местами интегрирования и с учетом (5.53) имеем
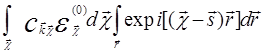 =
= 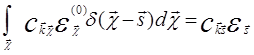 ,
,
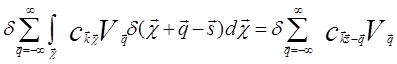 .
(5.55)
.
(5.55)
Используя (5.55), из (5.52) приходим следующему виду уравнения Шредингера
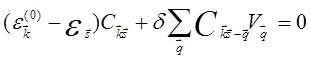 ,
(5.56)
,
(5.56)
из которого следует определить
значения энергии электронов с учетом взаимодействия их с ионами решетки {![]() } и волновые функции
} и волновые функции ![]() - функции Сks. Найдем возмущение k-го уровня,
и пусть в невозмущенном случае уровень
- функции Сks. Найдем возмущение k-го уровня,
и пусть в невозмущенном случае уровень ![]() не вырожден. Представим
не вырожден. Представим ![]() и
и ![]() в виде рядов по степеням малого параметра δ:
в виде рядов по степеням малого параметра δ:
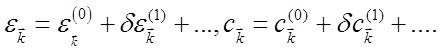 . (5.57)
. (5.57)
Подставляя (5.57) и группируя по степеням δ, получим
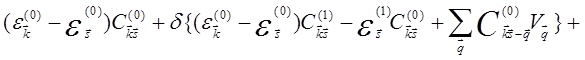 +
+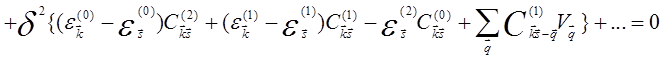 (5.56)
(5.56)
Поскольку уравнение (5.56) должно обращаться в ноль при любой степени δ, имеем
![]() (5.57a)
(5.57a)
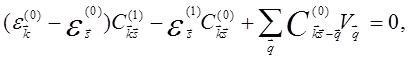 (5.57b)
(5.57b)
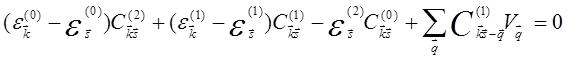 . (5.57c)
. (5.57c)
В уравнениях (5.57) необходимо отдельно рассмотреть случаи
![]() и
и ![]() .
.
В нулевом приближении из (5.57a) при ![]() имеем
имеем
![]() .
.
Откуда следует, что![]() произвольная функция своих аргументов.
произвольная функция своих аргументов.
В нулевом приближении из (5.57a) при ![]() следует, что
следует, что
![]() . (5.58)
. (5.58)
Следовательно,
![]() или
или ![]() . (5.59)
. (5.59)
В первом порядке теории возмущений из
(5.57b) при ![]() получаем
получаем
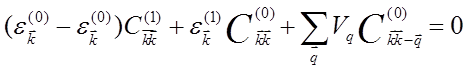 .
.
Отсюда следует, что![]() произвольная функция и ее можно
положить равной нулю
произвольная функция и ее можно
положить равной нулю ![]() , и с
учетом (5.59) получаем первую добавку к энергии свободных электронов за счет
взаимодействия их с решеткой
, и с
учетом (5.59) получаем первую добавку к энергии свободных электронов за счет
взаимодействия их с решеткой
![]() . (5.60)
. (5.60)
Таким образом, поправка первого порядка к энергии электрона есть постоянная величина, равная среднему значению возмущающего потенциала в основном состоянии.
В случае ![]() из (5.57b) получаем
из (5.57b) получаем
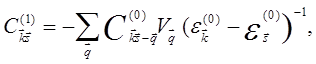
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.