Вместе с тем, я необходимо был вынужден прибегать к помощи движения особого рода – разделению прямой в точке и точки на прямой, для проявления того самого единства бесконечности и ограниченности (конечности), воплощением которого и является треугольник. Треугольник как бы берет от бесконечной окружности ее качество фигуры (в смысле замкнутости формы), а от конечного развернутого угла, - ограниченность этой самой фигуры.
Кроме того, аспект бесконечной фигуры (окружности), в треугольнике так же нашел свое воплощение и в бесконечном разнообразии всевозможных отличных друг от друга форм и размеров различных треугольников.
Теперь рассмотрим, каким же особым разделением и разделением чего, проявляется первая полноценная фигура геометрии – треугольник (рис. 8).
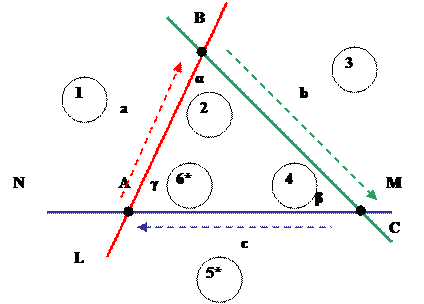 |
Рис. 8
1 - разделение точки А на прямой L, дало точку B и, соответственно, отрезок а;
2 - разделение прямой L в точке В, дало прямую М и, соответственно, угол α;
3 - разделение точки В на прямой M, дало точку C и, соответственно, отрезок b;
4 - разделение прямой M в точкеC, дало прямуюN и, соответственно, угол β, γ, а так же отрезок с.
Для полноты и завершенности построения, можно разделить точку С на прямой N, вернувшись обратно в точку А, и разделить прямую N в точке А, вернувшись обратно к прямой L, и тем самым завершить (замкнуть) полноценный цикл последовательного разделения прямой и точки.
Думаю, что совершенно очевидным является то обстоятельство, что если бы построение треугольника было начато не с разделения точки на прямой, а с разделения прямой в точке, то результат был бы получен тот же самый.
Вот такая необычная и простая последовательность разделений точки и прямой, позволила получить (проявить) фигуру совершенно нового качества, воплощающей в себе бесконечность формы и ограниченность угла.
Стоит обратить внимание на то, что в ходе формирования треугольника, третий его угол γ и третья его сторона c, определились необходимым образом, т.е. однозначно из всех предыдущих построений.
А это обстоятельство, явно указывает на то, что между величинами сторон и углов в треугольнике непременно существует строго определенная закономерная взаимосвязь.
Кроме всего прочего, в представленной трактовке образа треугольника, нет никакой необходимости заблаговременного введения такого понятия, как «плоскость», поскольку ее представление (образ) вполне естественно проистекает из самого треугольника. Поэтому треугольник, в конечном счете, воплощает собой актуальную двухмерность (площадь).
Треугольник по праву занимает место действительного Начала любой геометрической фигуры. Поскольку опыт моих исследований (на примере натуральных чисел) показывает, что Начало, есть половина Всего, то можно попытаться сформировать некоторые представления относительно истоков отдельных известных свойств треугольника.
В частности, можно понять, почему именно половину угловой величины окружности, содержит в себе всякий треугольник. Ведь треугольник, воплощает собой своеобразную Середину (поскольку является Началом …) между минимально возможной величиной угла луча (0), и максимально возможной угловой величиной окружности (2π), которая и составляет величину, тождественную – 2π/2 = π.
Подобное представление об угловой величине, воплощаемой любым треугольником, может существенно изменить порядок возведения единого здания геометрической науки.
Ведь равенство секущих и накрест лежащих углов, а так же понятие параллельных прямых, простым и естественным образом проистекает из представлений того же треугольника.
Сумма углов в треугольнике
Утверждение того, что треугольник воплощает собой угловую величину, тождественную π, можно доказать (более строго в общепринятом смысле), основываясь лишь на двух посылках:
- величина развернутого угла – π;
- угловая величина окружности или одного оборота - 2π.
И так, в завершении цикла построения треугольника, исходная прямая (L) совершит один полный оборот, возвращаясь в саму себя (посредством прямых M и N) (рис. 9).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.