Работа в MathCad: Практическое пособие, страница 3

3, … , m; j = 1, 2, 3, ..., n) - коэффициенты при неизвестных;  (i = 1, 2, 3, ..., m;     j = 1, 2, 3, ..., n) - правые части уравнений.

Определение

Решением СЛАУ называют совокупность значений неизвестных (х, х, ..., х), при подстановке которых в уравнения системы каждое из уравнений (2.1) обращается в тождество.

Пример

Рассмотрим следующую систему уравнений:

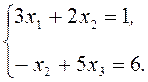
В системе

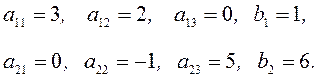
В качестве решения можно предложить следующий набор значений:

х= 1,  х= -1,  х= 1.

Действительно, в этом случае подстановка в систему дает

3×1 + 2(-1) = 1,   3 - 2 = 1,   1 = 1;

(-1)( -1) + 5×1 = 6,    1 + 5 = 6,   6 = 6,

т. е.  данный набор значений неизвестных обращает каждое из уравнений системы в тождество. Система линейных алгебраических уравнений (2.1) называется скалярной формой записи СЛАУ.

2.2.  Матричная форма записи системы линейных алгебраических уравнений

Для системы (2.1) введем следующие обозначения:

а) матрицу коэффициентов при неизвестных

А = ;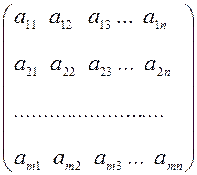

б) матрицу-вектор неизвестных

Х = ;

в) матрицу-вектор правых частей СЛАУ

В = .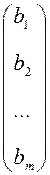

Используя операцию произведения матриц, рассмотренную в 1.2, система уравнений (2.1) может быть переписана в виде матричного уравнения:

АХ  = В.                         (2.2)

Матричная форма записи СЛАУ имеет определенные преимущества по сравнению со скалярной формой, которые заключаются в том, что для решения СЛАУ в матричной форме можно использовать развитый аппарат теории матриц. При изложении основных, наиболее часто используемых методов решения СЛАУ, будем полагать, что число уравнений равно числу неизвестных, и СЛАУ имеет единственный набор значений (х, х, ..., х), или, как принято говорить в этом случае, система имеет единственное решение.

Вопросы существования и единственности решения будут рассмотрены в дальнейшем. Поскольку многие методы решения СЛАУ опираются на понятие определителя, перейдем к элементам теории определителей.

2.3.   Элементы теории определителей

2.3.1   Определитель второго порядка

Понятие определителя возникло в связи с проблемой отыскания формул для решения линейных систем.

Рассмотрим квадратную матрицу второго порядка

А = .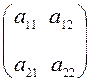

Возьмем произведение чисел, стоящих на главной диагонали, и вычтем из него произведение чисел, стоящих на второй диагонали. Получим выражение: .        

Определение

Полученное таким образом выражение называется определителем второго порядка, составленным из элементов матрицы  А (определителем матрицы  А), и обозначается

 = .

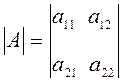Используют также обозначение вида

.

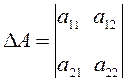Упражнение 4

Вычислить определитель второго порядка  .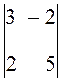

Решение

D =  3 × 5 - 2(-2) = 19.

2.3.2  Определитель третьего порядка. Правило треугольников

Возьмем матрицу третьего порядка

А = .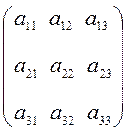

Определение

Определителем третьего порядка матрицы  А называется число, полученное из элементов матрицы  А по следующему правилу:      

D =  +  +  – ( +  + ).

Употребительна также следующая запись:

D = .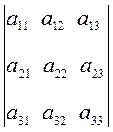

          Для вычисления определителя третьего порядка удобнее использовать правило треугольников (правило Саррюса), которое рассмотрим на конкретном примере.

Пример

Вычислить определитель третьего порядка  D = .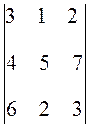 

По правилу Саррюса определитель дополняется двумя первыми столбцами:

.

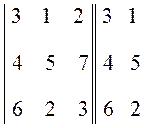В полученной структуре проводятся три левых и три правых диагонали:

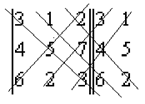
Произведение чисел, расположенных на главной и параллельных ей диагоналях, берется со знаком ²+², в то время как произведение чисел, расположенных на второй и параллельных ей диагоналях, берется со знаком  ²-²:

D = (3×5×3 + 1×7×6 + 2×4×2) - (6×5×2 +  2×7×3 + 3×4×1) = 103 – 114 = -11.

Таким образом, 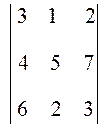  = -11.

Упражнение 5

Вычислить определитель

D =.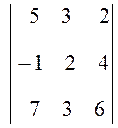

Решение

D = (5×2×6 + 3×4×7 + 2(-1) 3) - (7×2×2 + 3×4×5 + 6(-1) 3) = -6.

К сожалению, правило Саррюса не обобщается на вычисление определителей более высоких порядков. Для того чтобы вычислять определители порядков более высоких, чем третий, необходимо обратиться к свойствам определителей.

2.3.3   Упражнения для самостоятельной работы

Вычислить определители третьего порядка: