Работа в MathCad: Практическое пособие, страница 2

Видим также, что если A имеет размерность (m´n), а В имеет размерность (n´p), то размерность результирующей матрицы С = АВ будет равна (m´p).

Тем не менее, хотя произведение матриц в общем случае не обладает свойством коммутативности, оно имеет ряд других свойств:

1.  (А + В)С = АС + ВС;

2.  А(ВС) = (АВ)С;

3.  l(АВ) = (lА)В = А(lВ),  l Î R;

4.  QА = Q, где  Q - нулевая матрица.

1.4.  Единичная и обратная матрицы

Рассмотрим на конкретном примере произведение единичной матрицы E на квадратную матрицу А

,     ;

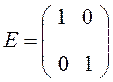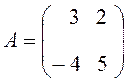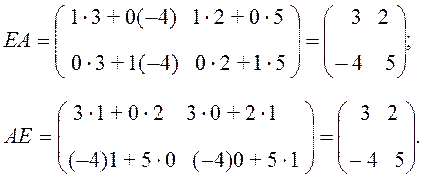
Из приведенного примера следует, что и в общем случае имеет место соотношение: EA = AE = A , т. е. единичная матрица Е всегда коммутативна и не изменяет перемножаемой матрицы А. Отметим, однако, справедливости ради, что праводиагональная единичная матрица, у которой все элементы, расположенные выше и ниже второй диагонали, равны нулю, а диагональные элементы равны единице, таким свойством не обладает. В самом деле,

.

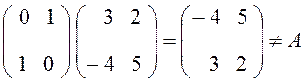Матрица Е является единственной матрицей, обладающей указанным свойством EA = AE = A.  Докажем это.

Предположим, что существуют две матрицы, Е и Е, которые имеют указанное свойство, т. е. ЕA = AЕ= A  и  ЕA = AЕ= A, где  А - произвольная квадратная матрица.

Рассмотрим произведение ЕЕ. Поскольку по предположению Е не меняет перемножаемой справа матрицы, то ЕЕ= Е. С другой стороны, аналогично рассуждая, получим, что ЕЕ= Е. Отсюда с необходимостью следует, что Е= Е, т. е. матрица  Е  является единственной, обладающей этим свойством.

Определение

Квадратная матрица А называется обратной по отношению к квадратной матрице  А, если  А А = Е, где  Е - единичная матрица.

Не задаваясь пока вопросом о существовании обратной матрицы  А, докажем, что матрица  А является перестановочной по отношению к матрице  А,  т. е.    А А = АА. Умножим  равенство   А А = Е  на матрицу   А  слева.  Получим:

 АА А =  АЕ = А.  Но тогда отсюда следует:  А(А А) = А, (АА) А =

= А,    АА = Е, что и требовалось доказать.

Докажем теперь единственность матрицы  А. Предположим, что существуют две различные матрицы,  и , обратные по отношению к матрице А.  Рассмотрим следующее произведение матриц:      А.

С одной стороны (А) = Е = , но с другой стороны  (А)= = Е= .  Таким образом, доказано: = , что и означает единственность обратной матрицы.

1.5.  Блочные матрицы и прямое произведение матриц

Вообще говоря, каждую матрицу можно рассматривать как совокупность матриц меньшей размерности. Данное утверждение справедливо для любых матриц. Отсюда вытекает следующее определение.

Определение

Матрица, состоящая из матриц меньшей размерности, называетсяблочной матрицей.

Пример

Пусть дана матрица

А = .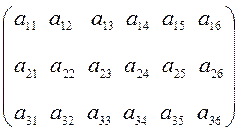

Рассмотрим следующие матрицы:

,  ,  ,

,   ,    .

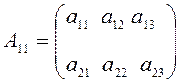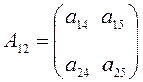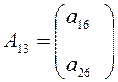Тогда матрица  А может быть представлена как блочная матрица

.

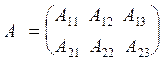Определение

Блочная матрица  А, имеющая структуру 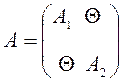, где Q - нулевая матрица, называется прямым произведением матриц  А и  А и обозначается  АÄ А.

Свойства прямого произведения матриц.

1. Сумма С двух прямых произведений матриц одинаковой структуры А и В является также прямым произведением матриц.

Доказательство

Пусть ,   .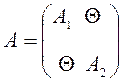

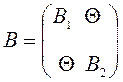Поскольку по условию порядок матрицы Асовпадает с порядком матрицы В, а порядок матрицы  А совпадает с порядком  матрицы В, то

С =А + В  =  +  =  = ,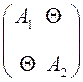

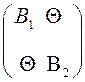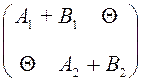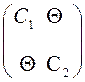где С= А+ В, С= А+ В и по определению матрица С является прямым произведением матриц  С и  С, т. е.  С = СÄ С.

2. Произведение  С  двух прямых произведений матриц одинаковой структуры  А и В  является также прямым произведением матриц.

Доказательство

Пусть ,   .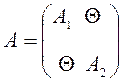

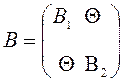Тогда  С = АВ =  =  = .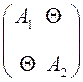

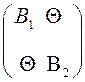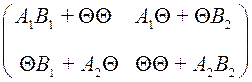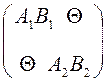Следовательно, матрица С является прямым произведением матриц АВ и АВ, т. е.  С = АВÄ АВ.

2.  СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ. ОСНОВНЫЕ ПОНЯТИЯ

2.1.  Определение системы линейных алгебраических уравнений

Определение

Системой линейных алгебраических уравнений (СЛАУ) называется система уравнений вида

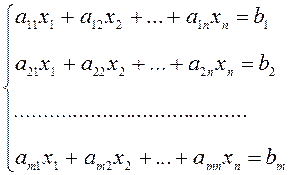,                                         (2.1)

где  m - число уравнений;  n -  число неизвестных  (х, х, ..., х);  (i = 1, 2,