Механическая колебательная система и методы ее анализа. Кинематика колебаний и возбуждающие нагрузки. Динамические характеристики системы - импеданс и адмитанс, страница 7

Разделение колебаний по признаку способа их возбуждения можно охарактеризовать следующей классификацией:

1) собственные колебания — колебания, вызванные начальным отклонением системы и протекающие без активного внешнего воздействия;

          2) вынужденные колебания — колебания, происходящие при действии внешних сил, преимущественно периодических;

3) связанные колебания — собственные или вынужденные, возникающие в сложных системах и отражающие взаимодействие отдельных частей системы между собой. Связанные колебания могут возникнуть, в частности, если между двумя раздельными системами, одна из которых колеблется, а другая находится в покое, внезапно будет создана упругая или иная кинематическая связь; в результате этого будут происходить связанные колебания обеих систем;

4) автоколебания – самоподдерживающиеся колебания, происходящие как при самовозбуждении, так и при начальном возбуждении системы извне, питание которых происходит за счет постоянного источника энергии и сил преимущественно непериодического характера.

5) колебания при параметрическом возбуждении, возникающие при периодическом изменении параметров системы (массы, коэффициентов упругости или др.).

а) Собственные колебания

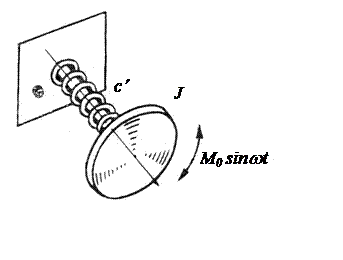
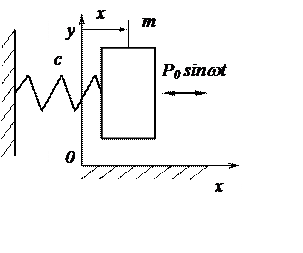
Система с одной степенью свободы обычно представляется в виде одной массы с пружиной. Такая система может совершать либо продольные колебания, либо крутильные колебания (рис. 3.17, 3.18). В первом случае пружина работает на растяжение-сжатие, во втором – на кручение. Теоретическое описание колебаний в обоих случаях одно и то же, с точностью дол обозначений.

В простейшем случае зависимость между перемещениям х (растяжением-сжатием) пружины и продольным усилием Р, а также между кручением q  и вращающимся моментом М является линейной.

Р = сх,                                                          (3.10)

М = с¢q,                                                          (3.11)

где     с – коэффициент жесткости на сжатие пружины;  с¢ - коэффициент жесткости на кручение пружины.

Сила  Р  и момент  М действуют на пружину.

	Рис. 3.17. Масса с пружиной, совершающая поступательные перемещения			Рис. 3.18. Масса с пружиной, совершающая вращательные движения

Дифференциальное уравнение колебаний получается на основании уравнений Лагранжа, если выразить кинетическую и потенциальную энергию системы масса-пружина. Для обоих случаев будем иметь

mx¢¢ + cx = 0,                                                          (3.12)

Jq¢¢ + с¢q = 0,                                                          (3.11)

где     m – масса тела;   J – момент инерции относительно оси вращения.

Существование простых зависимостей (3.10), (3.11) приводит к тому, что дифференциальные уравнения (3.12), (3.13) линейны, т.е. такие, в которые неизвестная величина и ее производные входят линейно. Такие дифференциальные уравнения имеют решения, описывающие гармонические колебания при совокупности гармонических колебаний. Колебания, описываемые решениями линейных дифференциальных уравнений, принято называть линейными.

Поскольку дифференциальные уравнения (3.12) и (3.13) с точностью до обозначений одинаковы, можно рассматривать только одно из них, например первое.

Решение дифференциального уравнения (3.12) выражает гармоническое продольное колебание

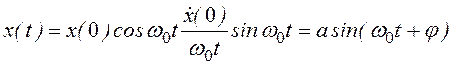              ,                                                          (3.13)

,     ,

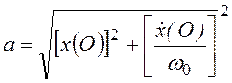где     x(0) и (0) - отклонение и скорость тела в  начальный момент t = 0; ω₀ = 2πf;   f - частота колебаний, Гц; φ - начальная фаза.

Движение, описываемое зависимостью (3.13), характеризует собственные колебания массы на пружине. Это движение может быть интерпретировано с помощью векторов, если применить комплексные числа. Введя, на основании формул Эйлера, обозначения

cosω₀t= ()/2,      sinω₀t = ()/2j

и подставив в (3.13), приведем к  комплексному выражению колебаний