Механическая колебательная система и методы ее анализа. Кинематика колебаний и возбуждающие нагрузки. Динамические характеристики системы - импеданс и адмитанс, страница 17

На практике часто имеют дело с так называемыми цепны­ми системами, которые получаются из простейших систем по­следовательным или параллельным соединением элементов. К этим системам относятся также разветвленные системы. Основным признаком цепной системы является то свойство, что она в любом месте может быть разделена на две части удалением только одной связи. Благодаря этому условие присоединения одной части к другой, может быть составлено при помощи только одного уравнения, которое выражает равенство нулю суммы импедансов или разности адмитансов одной и другой частей.

Более сложные системы, образующие кольца и сети, требуют вычисления переходных импедансов и адмитансов.

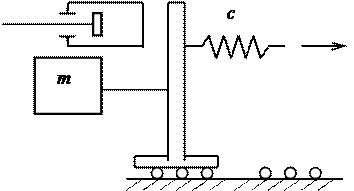
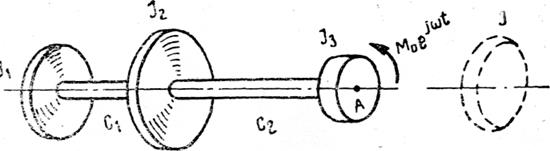
Для цепной системы, состоящей из последовательно чередующихся соединенных между собой вращающихся масс и элементов, обладающих упругостью на кручение (рис. 3.46,а), при приложении на конце пары с моментом  импеданс на основании постепенного наращивания получается из выражения

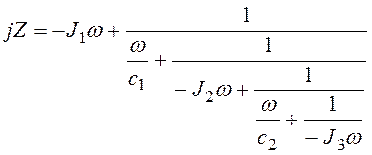                                                                                                                   (3.67)

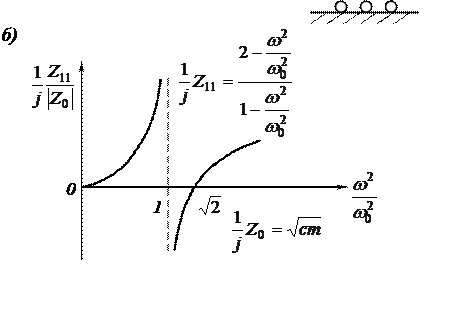
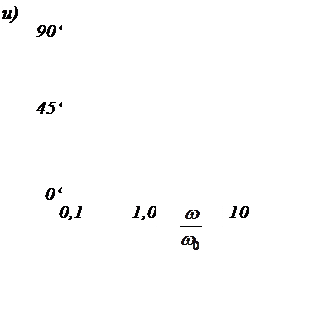
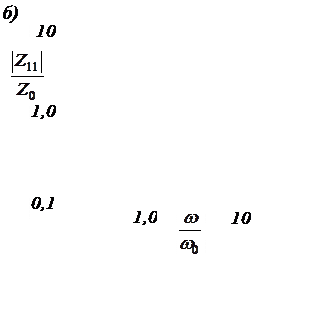
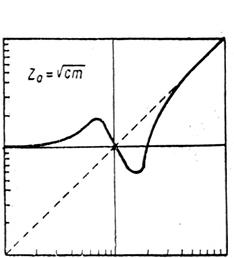
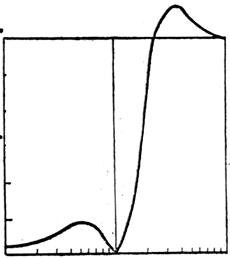
Вещественный множитель импеданса изображен на рис. 3.46,б. Он представляет собой функцию, имеющую три нуля (один из них при ω = 0) и два полюса.

Нули импеданса называются резонансными, а полюсы — антирезонансными угловыми частотами. Эти названия оправдываются следующим: резонансные частоты — частоты, с которыми колеблется система при нулевой возбуждающей силе, а при конечном значении силы система теряет общую жесткость, и  приобретает бесконечно большую скорость; антирезонансные частоты — частоты, соответствующие минимальной возбудимости, при которой жесткость теоретически бесконечно велика.

а)

V

с

                                                                                                         

					а)

 

m

ё

								r
											Р

 

                                                                                                                                                             

			Рис. 3.45. Та же система, что на рис. 3.44, но с дополнительным сопротивлением; ее импеданс
	Рис. 3.44. Система с комбинированным соединением без сопротивления и ее импеданс

 

3.9. Частоты собственных связанных колебаний

При помощи кривой импеданса легко решить задачу о собственных колебаниях системы, полученной из данной добавлением, например одной массы (показанной на рис. 3.46,а, пунктиром).

Импеданс массы будет . Условие соединения в точке А будет

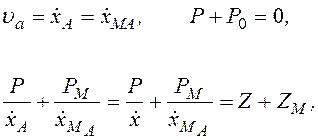
т.е. сумма импедансов системы и добавляемой массы равны нулю. Точки пересечения кривой импеданса системы и прямой I_w (пунктир) определяют угловые частоты, соответствующие собственным колебаниям связанной системы.

а)

	б)

 

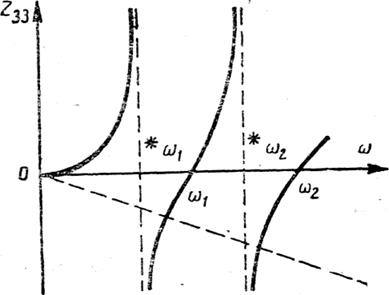
Рис. 3. 6. Импеданс сложной системы

3.10. Вынужденные колебания

В обычно встречающихся системах неупругое сопротивление, от которого зависит затухание колебаний, невелико и не оказывает существенного влияния на частоты собственных колебаний. Поэтому при определении частот связанных собственных колебаний систем можно, как правило, пользоваться выражением функций импеданса или адмитанса без учета сопротивления.