Свойством ортогональности (1.7) в одном атоме обладают волновые функции любых двух разных состояний электрона (Е1 ¹ Е2), в каком бы потенциальном поле он не находился.
Докажем это.
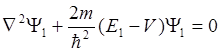 (1.8)
(1.8)
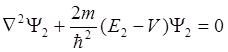 (1.9)
(1.9)
Умножим (1.8) на Y2, а (1.9) на Y1. Проинтегрируем по всему пространству и составим их разность (члены, содержащие V уничтожатся):
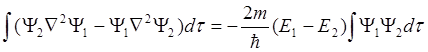 (1.10)
(1.10)
Интегрирование по dt включает в себя интегрирование по x, y и z от -µ до +µ. Сначала проинтегрируем по x (интегрирование по частям):
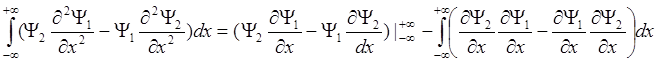 (1.11)
(1.11)
Интеграл справа равен нулю. При подстановке граничных условий в левую часть правого выражения она также обращается в нуль, т.к. волновая функция при x = ±µ равна нулю. Т.о. выражение 1.11 равно нулю. Аналогичный результат получается при интегрировании по y и z. Следовательно, нулю равна левая часть выражения 1.10. Отсюда:
![]() .
.
Если 1 и 2 состояния с разными энергиями, то Е1 ¹ Е2. Поэтому
![]() ,
,
что и требовалось доказать.
Используя принцип суперпозиции (линейная комбинация ортогональных функций), можно показать, что и в случае вырождения (Е1 = Е2) условие ортогональности функций Y1 и Y2 выполняется.
Из теоремы ортогональности вытекают важные для квантовой химии следствия:
- если Y1 и Y2 функции различной симметрии (соответствуют различным энергетическим уровням - s, p, d ...) одного и того же атома, то они ортогональны;
- каждая из вырожденных орбиталей одного типа симметрии ортогональна ко всем остальным орбиталям того же типа (рx ортогональна к рy и рz; dx2 ортогональна к остальным четырем);
- если Y1 и Y2 точные решения волнового уравнения и им соответствуют различные энергии Е1 и Е2, то они обязательно ортогональны.
- любые две волновые функции, вычисленные по методу линейных комбинаций Ритца, ортогональны, если построены из одних и тех же базисных функций.
1.2. Волновое уравнение.
Выведем волновое уравнение, исходя из волновой функции для движения свободного электрона. Для этого продифференцируем дважды волновую функцию для стоячей волны (без зависимости от времени).
![]() = A×sin
= A×sin![]() или
или ![]() = A×cos
= A×cos ![]() .
.
![]() = A
= A ![]() cos
cos ![]() ;
; 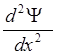 = - (
= - (![]() )2Asin
)2Asin ![]() .
.
![]() = A
= A ![]() sin
sin ![]() ;
; 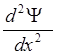 = - (
= - (![]() )2Acos
)2Acos
![]() .
.
Отсюда
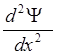 = - (
= - (![]() )2
)2![]() или
или
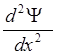 + (
+ (![]() )2
)2![]() =
0. (1.12)
=
0. (1.12)
Последнее
выражение и есть волновое уравнение для свободного электрона. В общем случае
каждое решение волнового уравнения надо умножить на временной множитель: sin2pnt или cos2pnt. Раскроем
смысл численного множителя перед волновой функцией ![]() в ур.
1.12. Из известного соотношения
в ур.
1.12. Из известного соотношения
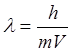 следует
следует 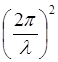 =
= 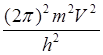 =
= 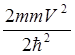 =
=![]() . Т.о. волновое уравнение принимает вид:
. Т.о. волновое уравнение принимает вид: ![]() +
+ 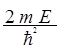
![]() = 0.
= 0.
Для
случая трехмерного пространства 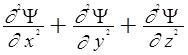 =
=![]() , где Ñ2 – оператор Лапласа, лаплассиан (читается: набла в
квадрате). Теперь волновое уравнение можно записать так:
, где Ñ2 – оператор Лапласа, лаплассиан (читается: набла в
квадрате). Теперь волновое уравнение можно записать так:
![]() +
+ ![]()
![]() =
0.
(1.13)
=
0.
(1.13)
Последнее уравнение аналогично уравнению, описывающему движение тела в классической механике (F = - kx) и фактически заменяет уравнение Ньютона (E = mV2/2). Кроме того, это уравнение применимо только к свободно движущимся частицам, где E - это кинетическая и в данном случае полная энергия. Т.к. полная энергия есть сумма кинетической (T) и потенциальной (V), то уравнение (1.13) можно зависать в следующем виде:
![]() +
+ ![]()
![]() =
0. (1.14)
=
0. (1.14)
Это и есть уравнение Шредингера, которое он написал впервые в 1926 г. Следует заметить, что в приближении геометрической оптики оно сводится к уравнению Якоби (описывающего траекторию движения тел с позиций классической физики). Кроме того, волновые функции, получаемые из ур. 1.9, оперируют скалярными величинами и не могут объяснить поляризацию фотонного потока. Более точную теорию разработал Дирак.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.