Квантовая химия как наука. Математический аппарат в квантовой химии. Решение волнового уравнения для некоторых частных случаев одномерного движения частицы, страница 10

          Наглядным примером дискретного набора значений МКД электрона в атоме является т.н. эффект Зеемана. Наличие МКД у электрона приводит к появлению у атома с таким электроном соответствующего магнитного момента (e - заряд электрона, c - скорость света):

m = 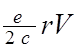.                                                                                (1.40)

Если электрон вращается в плоскости X0Y, то магнитный момент можно записать в следующем виде:

m_z =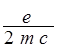 M_z.                                                                             (1.41)

Выражение (1.41) верно и в квантовой теории, где M_z может принимать значения кратные  (для р-состояния электрона - , 0 или ).

          Если электрон попадает в магнитное поле с напряженностью H, то к его энергии добавляется энергия взаимодействия с внешним магнитным полем:

W = m H = 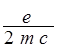 M_z H.(1.42)

          Появление дополнительных энергетических уровней, определяемых выражением 1.41, во внешнем магнитном поле и называется эффектом Зеемана.

W = + Н

W = 0

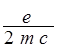
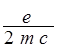
W = -  Н

Рис. 1.2. Эффект Зеемана для р-состояния электрона.

          Если электрон находится в d-состоянии, то  компонента М_z МКД может принимать пять значений: 2; ; 0; -; -2. В магнитном поле d-уровень по энергии расщепляется на 5 подуровней.

          Удобно толковать возможные значения М_z с помощью понятия пространственного квантования. Значения, которые может принять МКД, определяется выражением: l, где l - орбитальное квантовое число. Максимальное значение l, как известно, равно (n - 1), где n - главное квантовое число. По отношению к оси Z вектор МКД может принимать только определенные (дискретные) ориентации, при которых его проекции будут кратны величине . Возможно (2l + 1) различных значений проекции (см. рис. 1.3). На такое же число уровней расщепляется основной уровень в магнитном поле.

                  р-состояние              d-состояние

          Рис.1.3. Пространственное квантование МКД для p- и d-состояний.

          1.9. Спин электрона.

          Как указывалось выше, при попадании орбитального электрона в магнитное поле  основной энергетический уровень должен расщепляться на нечетное число подуровней (2l + 1). Однако был обнаружен и аномальный эффект Зеемана, т.е. было обнаружено расщепление энергетических уровней некоторых атомов (в частности, щелочных металлов) на четное число подуровней. Аномальный эффект Зеемана – это не единственное явление в области магнетизма, которое оставалось необъяснённым. Были ещё гиромагнитные аномалии. Отношение магнитного момента к механическому оказалось примерно вдвое больше предсказываемой величины (отношение заряда электрона к его массе). Затруднение было разрешено предположением Гоудсмита и Уленбека  в 1925 г. о том, что электрон вращается вокруг собственной оси и имеет собственный МКД, который был назван спином (s). При этом они приписали электрону собственный МКД, равный половине квантовой единицы . Для атомов с одним s-электроном (который не имеет орбитального МКД) расщепление происходит на два подуровня (2 = 2s + 1 и s = ½) (см. рис.1.4).

Таким образом, компоненты спинового МКД в направлении оси Z могут принимать следующие два значения:

                                        M_zs = ±.                                                    (1.43)

          Из величины расщепления можно определить значение спинового магнитного момента:

                                   m_s =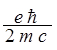.                                                          (1.44)

          Т.к. спиновое квантовое число s = 1/2, то спиновый магнитный момент ()  и МКД в 2 раза больше орбитального.