Волновое уравнение для двух электронов. Методы решения волнового уравнения, страница 2

Здесь электрон № 1 находится в состоянии 2, а электрон № 2 в состоянии 1. Этой волновой функции соответствует та же энергия – Е = Е₁ + Е₂. Т.о. существует две функции, принадлежащие одной и той же энергии. Этот вид вырождения связан с возможностью обмена местами электронами, т.е. имеет место полная симметрия волнового уравнения относительно обозначений электронов. Это называется обменным вырождением.

          Для любой квантовой системы, содержащей несколько одинаковых частиц (электронов, протонов, фотонов и т.д.), различить эти частицы невозможно. Эта неразличимость приводит к тому, что при перестановке индексов одинаковых частиц в волновой функции плотность вероятности меняться не должна. Однако, при такой перестановке сама волновая функция может вести себя различно. Используя принцип суперпозиции, можно  образовать любую линейную комбинацию решений 2.3 и 2.7, которая тоже будет решением ур.2.1. Например:

Y₊ = Y₁(1) ×Y₂(2) + Y₁(2) ×Y₂(1);                                                   (2.8)

Y_- = Y₁(1) ×Y₂(2) - Y₁(2) ×Y₂(1).                                                    (2.9)

Данные решения более универсальны, чем предыдущие, т.к. их  физический смысл не изменяется от перестановки электронов № 1 и № 2. Однако перестановка номеров электронов в ур. 2.8 и 2.9 даёт различный результат:

Y₊(1;2) = Y₊(2;1) ;                                                                          (2.10)

Y_-(1;2)  = -Y_-(2;1).                                                                        (2.11)

При этом функции типа 2.10 называют симметричными, а 2.11 – антисимметричными. Изменение знака в равенстве 2.11 не существенно, т.к. физический смысл имеет Y² (вероятность нахождения электрона в определенной точке пространства). Вследствие независимости Y²  от перестановки электронов при решении конкретных задач следует использовать именно волновые функции 2.8 и 2.9. В квантовой механике физическое состояние тождественных частиц могут описывать только такие волновые функции, которые при замене частиц местами являются либо симметричными, либо антисимметричными. Это требование –  математическая формулировка принципа тождественности микрочастиц.

          Интересно отметить, что математическое выражение антисимметричной волновой функции 2.9 соответствует записи определителя (детерминанта) квадратной матрицы:

          Y_- = .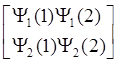

          Если произвести нормировку (), то получим нормировочный коэффициент .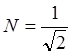

          В случае многоэлектронной системы волновая функция такого типа будет иметь вид:

          .

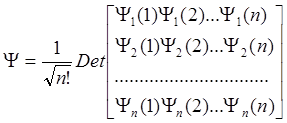Такая функция называется детерминантом Слетера.

3.  ПРИНЦИП ИСКЛЮЧЕНИЯ ПАУЛИ

          До сих пор при написании волновых функций для электрона в атоме мы учитывали только орбитальное движение. Однако, как известно, электрон имеет и спиновый МКД. Для полноты описания состояния электрона в атоме волновая функция должна учитывать и это свойство. Напомним, что спиновый момент электрона может принимать значения m_sz = ±1/2.

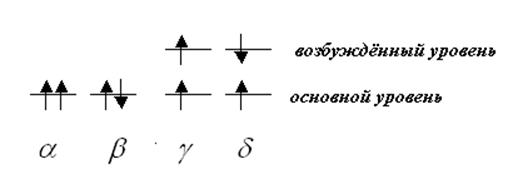
            Рис. 3.1 Возможные состояния спинов электронов в атоме гелия.

На рис. 3.1 представлены 4 возможных состояния спинов электронов в атоме He. Основное состояние Не в магнитном поле не расщепляется, что говорит о том, что в основном состоянии электроны в атоме гелия антипараллельны (b-случай). Экспериментально обнаружено, что при возбуждении возможны g и d-состояния. Триплет a не обнаружен. Проанализировав все мыслимые комбинации электронов в атомах гелия, лития и других элементов, и сверив их с экспериментальными данными, Паули пришел к выводу, что не может быть двух (и более) электронов в атоме (или молекуле) в одном и том же состоянии, если учитывать и орбитальный и спиновый моменты.