



































1 и 2 теоремы Вейерштрасса
Первая теорема
Вейерштрасса : Всякая непрерывная
функция ![]() , заданная на отрезке
, заданная на отрезке ![]() , ограничена, т.е.
, ограничена, т.е. ![]() числа
m и M такие, что
числа
m и M такие, что ![]() .
.
Доказательства: Докажем ограниченность сверху, т.к. снизу аналогично!!!
1) ![]() -ограничена
сверху,
-ограничена
сверху, ![]() - это надо доказать. Предположим, что это
неверно.
- это надо доказать. Предположим, что это
неверно.
2) т.е. ![]() , такое что
, такое что ![]()
3) Возьмем ![]() , что
, что ![]()
4) Меняем ![]() получаем последовательность
получаем последовательность ![]() . Выделяем сходящуюся
подпоследовательность:
. Выделяем сходящуюся
подпоследовательность: ![]()
![]()
5) т.к. ![]() - непрерывная
- непрерывная![]()
6) Если в 3) взять n=1 ,
![]() но
но ![]() ,
противоречие => 2) – не верно т.к. верно1) => теорема доказана для M, а
для m – аналогично
,
противоречие => 2) – не верно т.к. верно1) => теорема доказана для M, а
для m – аналогично
Вторая теорема
Вейерштрасса: Всякая непрерывная
функция![]() , достигает своих наибольшего и наименьшего
значений, т.е. если
, достигает своих наибольшего и наименьшего
значений, т.е. если 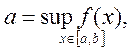
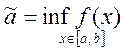 , то
, то ![]()
![]() и
и ![]()
![]() , что
, что ![]() а
а ![]()
Доказательство: Только для sup, т.к. inf
аналогично. Надо доказать, что![]()
![]() ,
такие что
,
такие что ![]() где
где ![]() .
Допустим, такой точки нет, т.е.
.
Допустим, такой точки нет, т.е. ![]() . Рассмотрим
. Рассмотрим 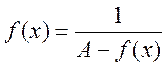 ,
, ![]() для
для ![]() по построению и
по построению и ![]() -
непрерывна, т.к. 1-непрерывна и разность тоже =>
-
непрерывна, т.к. 1-непрерывна и разность тоже => ![]() -непрерывна
=> по 1-ой теореме Вейерштрасса она ограничена сверху, т.е.
-непрерывна
=> по 1-ой теореме Вейерштрасса она ограничена сверху, т.е. ![]() А1>0, что
А1>0, что ![]()
![]() , подставим вместо
, подставим вместо ![]()
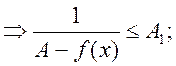
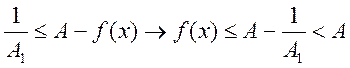
Достаточные условия дифференцируемости функции
Теорема:
Пусть функция ![]() имеет в области
имеет в области ![]() непрерывные
частные производные
непрерывные
частные производные 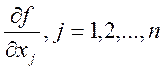 . Тогда эта функция диф-ма в D.
. Тогда эта функция диф-ма в D.
Доказательство: сначала докажем для функции двух переменных: ![]() . Существуют
. Существуют 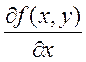 ,
, 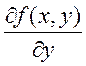 непрерывные в D. Надо
доказать, что
непрерывные в D. Надо
доказать, что 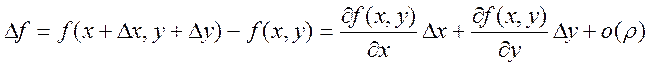 , где
, где ![]() .
Рассмотрим
.
Рассмотрим
![]()
![]() {т.к. существуют непрерывные производные по
х
{т.к. существуют непрерывные производные по
х ![]() формула Лагранжа о конечных приращениях}
формула Лагранжа о конечных приращениях}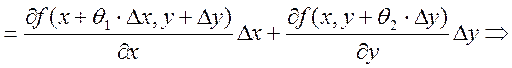

 -
-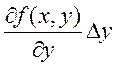 +
+ +
+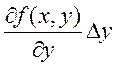 =
= +
+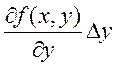 +
+![]() +
+![]() ,
где
,
где 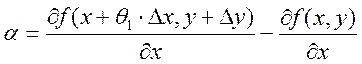 , а
, а 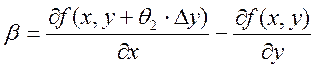 .
Теперь докажем, что
.
Теперь докажем, что ![]()
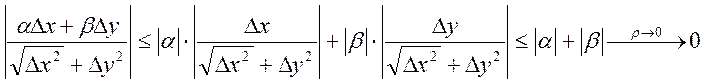 . Т.к.
частные производные непрерывны
. Т.к.
частные производные непрерывны ![]() . Поэтому,
. Поэтому, 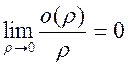 ч.т.д.
ч.т.д.
Теперь докажем для функции
трех переменных: ![]() . Существуют
. Существуют 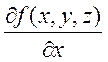 ,
,  ,
, 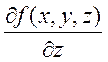 непрерывные в D,
непрерывные в D,  , где
, где ![]() - это
надо доказать!
- это
надо доказать! ![]()
![]() (по
Лагранжу)
(по
Лагранжу) 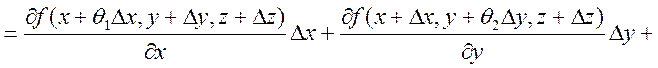
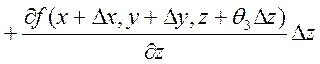 , где
, где ![]() ,
, 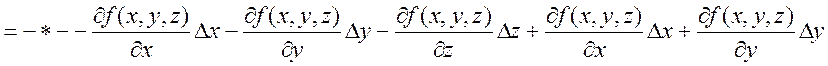
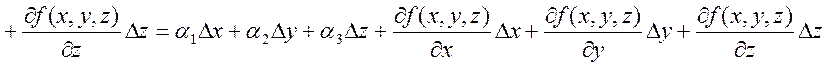 . Покажем, что
. Покажем, что ![]() ,
(разделим на
,
(разделим на ![]() и докажем, что
и докажем, что ![]() )
) 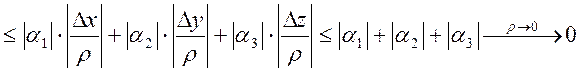
Теперь докажем для n: ![]()
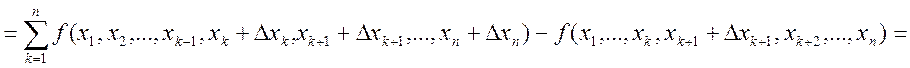
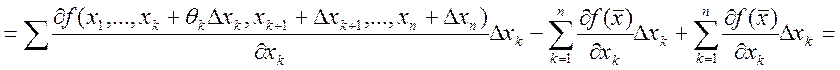
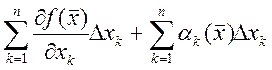 , где
, где 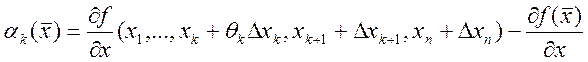 . Докажем
. Докажем
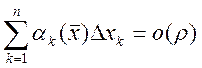 , где
, где ![]() .
. 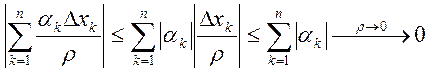 . Ч.т.д.
. Ч.т.д.
Интегралы, зависящие от параметра
Рассмотрим ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]()
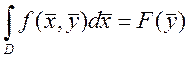
Опр.: функция ![]() - есть интеграл,
зависящий от параметра
- есть интеграл,
зависящий от параметра ![]() .
.
Ех:  -
это функция.
-
это функция.  , при a>0 -
сходится
, при a>0 -
сходится
Мера Жордана.
Опр.: ![]() ,
,
![]() - в этом пространстве
- в этом пространстве ![]() .
.
Сетка: строятся точки (узлы):
![]() . Берётся набор
. Берётся набор ![]() .
.
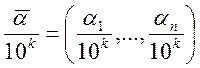 - точки строятся – узлы. Сначала
рассмотрим узлы для n=1
- точки строятся – узлы. Сначала
рассмотрим узлы для n=1![]()
![]() -
прямая. Чем больше k, тем больше (гуще) сетка.
-
прямая. Чем больше k, тем больше (гуще) сетка. 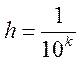 - шаг
сетки,
- шаг
сетки, 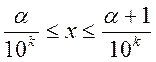 - элемент сетки.
- элемент сетки.
Мера Жордана:
1) Каждый кубик имеет объём 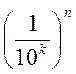 - аксиома!
- аксиома!
2) Если тело состоит из
кубиков ![]() объём тела = сумме объемов кубиков.
объём тела = сумме объемов кубиков.
1. берём минимальную область, состоящую из квадратиков, которая содержит фигуру.
2. берём максимальную область, которая содержится в фигуре.
3. ![]() и
смотрим куда стремится (1) и (2).
и
смотрим куда стремится (1) и (2).
Пусть Е – произвольное
множество, такое что![]()
1) ![]() ,
и т.ч.
,
и т.ч. ![]() ,
, ![]() .
.
2) Берём ![]() , т.ч.
, т.ч. ![]()
![]() . Получ.
. Получ. ![]() и
и ![]() - это объёмы
- это объёмы![]() и
и![]() соответственно.
соответственно. ![]() возрастает
при
возрастает
при ![]() ,
, ![]() убывает
при
убывает
при ![]() .
.
Это две монотонные числовые
последовательности. ![]() , а
, а ![]() .
.
Опр:.: нижняя мера Жордана - ![]() . Верхняя мера Жордана -
. Верхняя мера Жордана - ![]()
Опр.: множество ![]() измеримо по Жордану, если
измеримо по Жордану, если ![]()
![]() . И мера обозначается
. И мера обозначается![]()
Свойства меры Жордана:
1) мера Е, ![]() (Ех: кривая на плоскости). Если
(Ех: кривая на плоскости). Если ![]() Е – множество меры нуль.
Е – множество меры нуль.
2) если ![]()
![]()
3) пусть ![]() - множества (измеримые)
- множества (измеримые) ![]() , такие что
, такие что ![]() (
(![]() ). Тогда
). Тогда 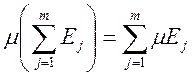 ,
, 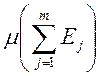 - это
- это 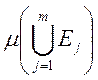 .
Иногда эти свойства объединяют в аксиомы.
.
Иногда эти свойства объединяют в аксиомы.
Теорема: для того чтобы множество ![]() было
измеримо по Жордану необходимо и достаточно, чтобы оно было ограничено, и
было
измеримо по Жордану необходимо и достаточно, чтобы оно было ограничено, и ![]() , где
, где ![]() -
граница множества Е.
-
граница множества Е.
(Граничная точка ![]() в любой окрестности точки есть как точки из
Е, так и точки не принадлежащие Е)
в любой окрестности точки есть как точки из
Е, так и точки не принадлежащие Е)
Следствие: если ![]() и
и ![]() -
непрерывна в D (D – компакт), то график функции
-
непрерывна в D (D – компакт), то график функции ![]() имеет (n+1) меру
Жордана равную 0
имеет (n+1) меру
Жордана равную 0
Множества уровня функций. Градиент.
Рассмотрим функцию ![]() ,
, ![]() .
.
Опр.: множество ![]() такое,
что
такое,
что ![]() , называется множеством уровня
, называется множеством уровня ![]() функции
функции ![]()
(Ex: высота над
уровнем моря ![]() )
)
![]() , т.к.
функция принимает всего одно значение, а было бы два
, т.к.
функция принимает всего одно значение, а было бы два ![]() ex:
ex: ![]() ,
, ![]() окружность,
окружность,
![]() точка,
точка, ![]() .
. ![]() - сфера, радиусом -
- сфера, радиусом - ![]() , если
, если ![]()
Опр.: вектор функция  ,
, ![]() - градиент функции
- градиент функции ![]() и
обозначается
и
обозначается ![]() .
.
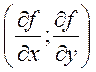 - это
градиент на плоскости.
- это
градиент на плоскости.
Векторные(физические) поля – градиенты некоторых функций.
Градиент ![]() плоскости
плоскости
1) градиент всегда направлен ![]() поверхности уровня (
поверхности уровня (![]() производная)
производная)
2) наибольшее изменение
функции происходит по направлению градиента 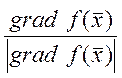 , в
точке
, в
точке ![]() существует направление.
существует направление.
Докажем эти два факта:
1) будем считать, что прямая ![]() поверхности – значит она
поверхности – значит она ![]() плоскости касательной к этой поверхности в
этой точке.
плоскости касательной к этой поверхности в
этой точке.
Прямая должна (необходимо и
достаточно) быть ![]() любой касательной к любой кривой
в этой точке – тогда прямая
любой касательной к любой кривой
в этой точке – тогда прямая ![]() поверхности.
поверхности.
2) Рассмотрим множество
уровня: ![]() ,
, ![]() ,
, ![]() и при
и при ![]() ,
, ![]() ,
, ![]() меняется,
а функция =
меняется,
а функция = ![]()
![]() диф-ем
диф-ем ![]()
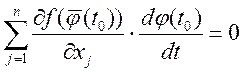
 -
касательная к поверхности, причем любой.
-
касательная к поверхности, причем любой.![]()
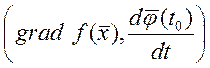 =0.
=0.
Поэтому прямая ортогональна ![]() градиент.
градиент.
Всегда ортогонален поверхности уровня.
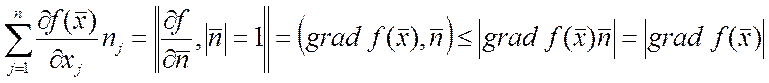 , т.е.
, т.е. ![]() ,
, 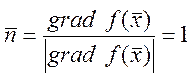 . Подставим
:
. Подставим
: 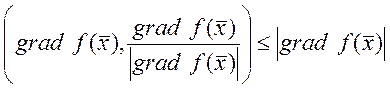 , а для любого другого направление меньше.
Поэтому по градиенту
, а для любого другого направление меньше.
Поэтому по градиенту ![]() изменение.
изменение.
Определение интеграла Римана для функции многих переменных
![]() зависит
от выбора точки, мелкости разбиения. Диаметр множества -
зависит
от выбора точки, мелкости разбиения. Диаметр множества - ![]() .
. ![]() -
наибольший диаметр разбиения.
-
наибольший диаметр разбиения.
Определение: 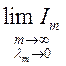 , если он существует и не зависит от
способа разбиения Е, и не зависит от точки
, если он существует и не зависит от
способа разбиения Е, и не зависит от точки ![]() , то этот
предел
, то этот
предел 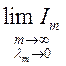 - интеграл Римана и обозначается символом
- интеграл Римана и обозначается символом 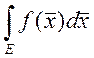
Определение кратного интеграла
Мы будем рассматривать
функции ![]() ,
, ![]()
1) Е – ограниченное измеримое по Жордану множество Rn
2) ![]() ,
, ![]() ,
, ![]()
Производная по направлению.
![]() ,
, ![]() ,
, ![]() .
Иногда пишут
.
Иногда пишут ![]() .
. 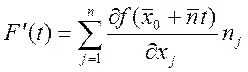 ,
, ![]() - производная по направлению m.
- производная по направлению m. 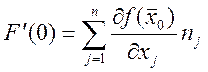 производная функция
производная функция ![]() в
точке
в
точке ![]() в направлении
в направлении ![]() .
. 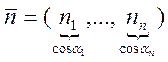
На плоскости ![]() . В пространстве
. В пространстве ![]() ,
,
![]() ,
, 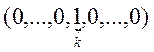 - это
производная по k – ому направлению
- это
производная по k – ому направлению
Определения
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.