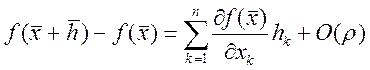 ,
где
,
где 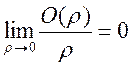
Ряды Фурье, коэффициенты Фурье. Формула Фурье.
Функциональные ряды:
Ряд: ![]() -
это могут быть различные функции, числа, комп. числа…
-
это могут быть различные функции, числа, комп. числа…
Функциональный ряд, ![]() - функции
- функции ![]() . Т.е.
. Т.е. ![]() - последовательность функций. Тогда
- последовательность функций. Тогда 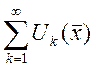 - функциональный ряд. Если функции не
зависят от
- функциональный ряд. Если функции не
зависят от ![]() числовой ряд.
числовой ряд.
Приложение имеют два типа рядов:
1) степенные 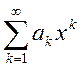 ,
, ![]() ; если
компакт
; если
компакт 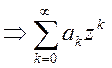
2) тригонометрические 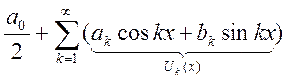 ,
, ![]() Это
периодические функции
Это
периодические функции ![]() ).
). ![]() - это
спектр, а
- это
спектр, а ![]() - гармоника.
- гармоника.
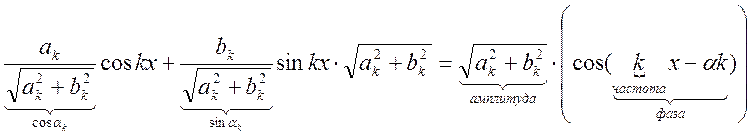 .
.
Фактически, интеграл – это сумма ряда.
Главный вопрос о сходимости ![]() рассматривают
рассматривают 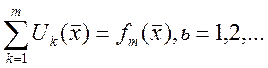 -
конечные суммы.
-
конечные суммы. ![]() последовательность функций – это
частичная сумма ряда.
последовательность функций – это
частичная сумма ряда.
Опр.: ряд (функциональный)
называется сходящимся в D, если ![]() , существует
, существует ![]() . Если это так, то
. Если это так, то ![]() пишут:
пишут:
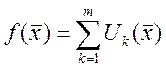 - сумма ряда. Если это не так
- сумма ряда. Если это не так ![]() расходящийся!!! Если два ряда сходятся
расходящийся!!! Если два ряда сходятся ![]() сходится и их сумма. При изучении этих
рядов выявилось, что простой сходимости недостаточно
сходится и их сумма. При изучении этих
рядов выявилось, что простой сходимости недостаточно ![]() равномерная
сходимость.
равномерная
сходимость.
Опр.: функциональный ряд 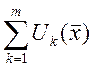 является
равномерно сходящимся в D, если для
является
равномерно сходящимся в D, если для ![]() (независящий от
(независящий от ![]() ) такие, что
) такие, что ![]() , для
, для ![]() и
и ![]() .
.
Имеют место теоремы (без доказательства):
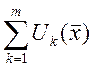 - сходится, а
- сходится, а 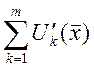 -
сходится равномерно на
-
сходится равномерно на 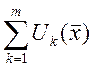 =
=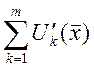
Запишем тригонометрический
ряд: 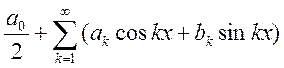 . По теореме Эйлера
. По теореме Эйлера 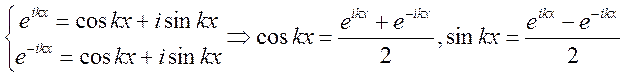 .
Подставим в формулу ряда
.
Подставим в формулу ряда ![]()
![]()
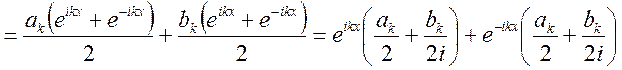
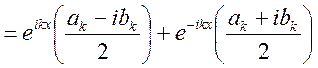
![]() ряд
ряд
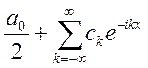 - если
- если 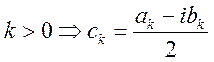 , если
, если
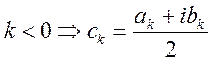 ,
, ![]() -
степенной ряд в комплексной плоскости. Т.е. ряды тригонометрические – это степенные
ряды такого типа, когда
-
степенной ряд в комплексной плоскости. Т.е. ряды тригонометрические – это степенные
ряды такого типа, когда ![]()
Лемма: если тригонометрический ряд (1) 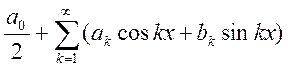 сходится равномерно на отрезке
сходится равномерно на отрезке ![]() к
к ![]() . Тогда
имеет место формулы Фурье:
. Тогда
имеет место формулы Фурье: 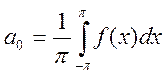 ;
; 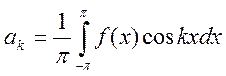 , а
, а 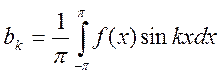 . Это коэффициенты
Фурье.
. Это коэффициенты
Фурье.
Доказательство:
Коэффициенты ряда (1) –
непрерывные функции, т.е. тригонометрический ряд, состоящий из непрерывных
функций, и ряд сходящийся равномерно ![]() - функция непрерывна,
поэтому интегралы
- функция непрерывна,
поэтому интегралы 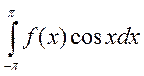 и
и 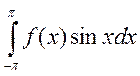 существует.
Проинтегрировав ряд почленно: (*)
существует.
Проинтегрировав ряд почленно: (*)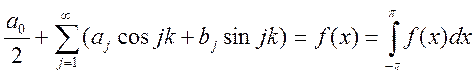 .
.
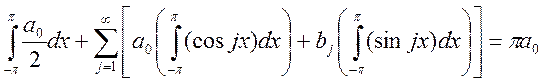 . Т.е.
. Т.е.
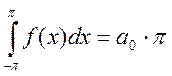 , т.е.
, т.е.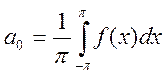 .
Умножим обе части равенства (*) на
.
Умножим обе части равенства (*) на ![]() . (т.к. ряд сходится
равномерно
. (т.к. ряд сходится
равномерно![]() сейчас тоже равномерно)
сейчас тоже равномерно) ![]() интегрируем почленно по х
интегрируем почленно по х ![]()
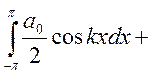
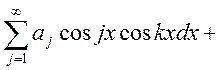
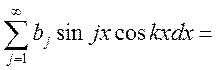
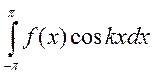
1) Докажем это (что всё равно
0, за исключением ![]() )
)
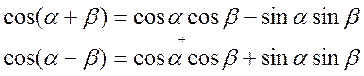
![]()
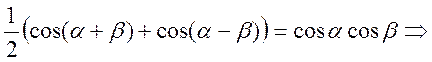 тогда
тогда 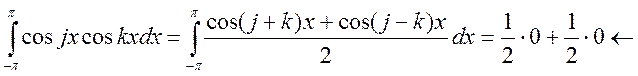 если
если ![]() , т.к.
, т.к. ![]() - положит. Поэтому весь интеграл при
- положит. Поэтому весь интеграл при ![]() равен
равен 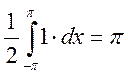
2) 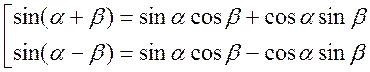
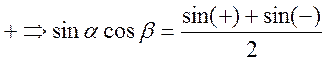 . Тогда
. Тогда 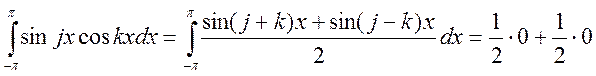 . В
итоге, весь интеграл
. В
итоге, весь интеграл ![]()
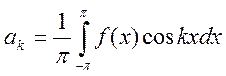 . Чтобы
посчитать
. Чтобы
посчитать ![]() надо (*) умножить на
надо (*) умножить на ![]() и аналогично. Всё, лемма доказана!
и аналогично. Всё, лемма доказана!
Опр.: пусть ![]() интегрируема на отрезке
интегрируема на отрезке
![]() функция, и
функция, и ![]() и
и ![]() определены равенствами
определены равенствами 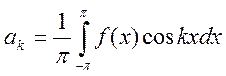 и
и 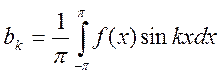 .
Тогда ряд (тригонометрический)
.
Тогда ряд (тригонометрический) 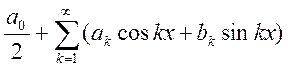 называется рядом Фурье
для
называется рядом Фурье
для ![]()
Свойства кратных интегралов
1. 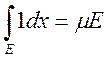 , если
, если ![]()
2. 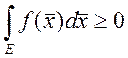 , если
, если ![]() ,
, ![]()
3. 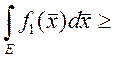
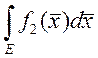 ,
если
,
если ![]() . Если суммируем
. Если суммируем ![]()
![]() и
и ![]() - две
последовательности
- две
последовательности![]()
![]()
![]() при одинаковом разбиении и одинаков.
при одинаковом разбиении и одинаков. ![]() .
.
4. 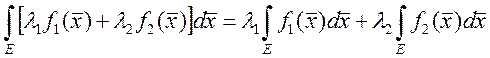
5. Если ![]() ,
, ![]() , то
, то 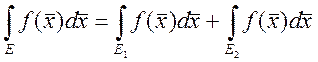
6. Если ![]() и
и ![]() , тогда
, тогда 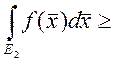
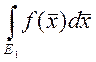
7. Если ![]() - непрерывна в D,
где D – область
- непрерывна в D,
где D – область ![]() , и
, и ![]() и
и 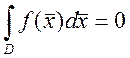 , то
, то ![]() в D
в D
Доказательство: пусть ![]() ,
, ![]() пусть
для определения
пусть
для определения ![]() . Т.к. функция непрерывна
. Т.к. функция непрерывна ![]() существует окрестность
существует окрестность![]() , где
, где ![]() , для
, для ![]()
![]()
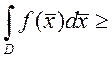
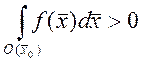
8. Если ![]() ,
, ![]() - непрерывна в D и
- непрерывна в D и 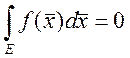 , для
, для ![]() , то
, то ![]() в D
в D
Доказательство: ![]() ,
, ![]() пусть
для определения
пусть
для определения ![]() . Т.к. функция непрерывна
. Т.к. функция непрерывна ![]() существует окрестность
существует окрестность![]() , где
, где ![]() , для
, для ![]()
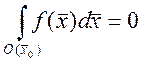 , но с другой стороны
, но с другой стороны 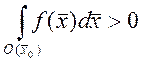
![]() противоречие.
противоречие.
9. Если ![]() непрерывна в D,
непрерывна в D, ![]() , и
, и 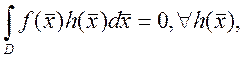
![]() - непрерывна в D, то
- непрерывна в D, то ![]() в D
в D
Доказательство: (отриц) ![]() ,
, ![]() ,
, ![]() и
и ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.