![]() -
непрер.,
-
непрер., ![]() , что
, что ![]() и
и ![]()
И ![]() ,
, ![]()
Если подставим, то получим,
что с одной стороны ![]() , а с другой
, а с другой ![]()
10. (теорема о среднем)
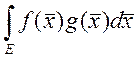 ,
, ![]() ,
, 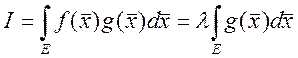 -
- ![]() число
число ![]() .
. ![]() . Тогда
. Тогда 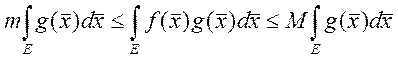 ,
, ![]() - это всё числа. Если
- это всё числа. Если ![]() - непрерывна
- непрерывна![]() достигается,
тогда
достигается,
тогда ![]() теорема о среднем
теорема о среднем 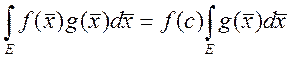
11. Неравенство Коши – Буняковского:
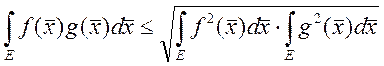
Доказательство: множество
интегрируемых функций образует линейное пространство ![]() вводим
скалярное произведение
вводим
скалярное произведение  . А там выполнено
неравенство К-Б.:
. А там выполнено
неравенство К-Б.: ![]() . Если подставим, то получим, то
что нужно. Если
. Если подставим, то получим, то
что нужно. Если 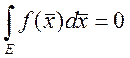 для
для ![]() ,
, ![]() - бывает.
- бывает.
Теорема Гельмгольца
Теорема
Любое непрерывно диф-мое
векторное поле ![]() можно представить в виде
можно представить в виде ![]() , где
, где ![]() (безвихревое),
а
(безвихревое),
а ![]() (потенциальное)
(потенциальное)
Доказательство: возьмём ![]() класса
класса ![]()
Положим ![]() , а
, а ![]() .
. ![]() - это доказано (в утверждениях) –
выполнено. Потребуем, чтобы
- это доказано (в утверждениях) –
выполнено. Потребуем, чтобы ![]() , т.е
, т.е ![]() , т.е
, т.е ![]() - это
условие, чтобы теорема была верна. (это дифур второго порядка – уравнение
Пуассона (оно имеет решение)). Поэтому теорема Гельмгольца имеет место!
- это
условие, чтобы теорема была верна. (это дифур второго порядка – уравнение
Пуассона (оно имеет решение)). Поэтому теорема Гельмгольца имеет место!
Теорема Дирихле.
Теорема:
Пусть периодическая функция ![]() имеет непрерывную производную на
имеет непрерывную производную на ![]() . Тогда её ряд Фурье к ней сходится.
. Тогда её ряд Фурье к ней сходится.
Доказательство:
Сначала докажем
тригонометрическое тождество: 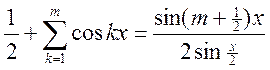 . Рассмотрим
. Рассмотрим 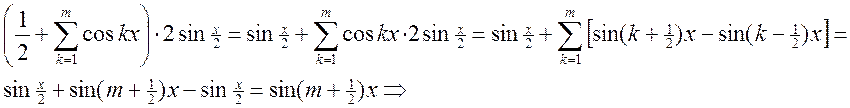
Тождество доказано!
Если проинтегрировать обе
части тождества от ![]() до
до ![]()
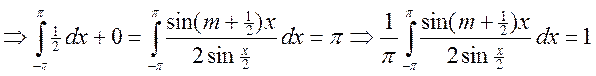 , чётная по х
, чётная по х ![]() это =
это = 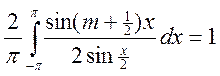 .
.
Продолжение доказательства теоремы:
сам ряд 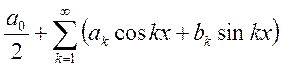 ,
, 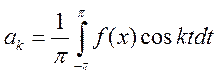 ,
, 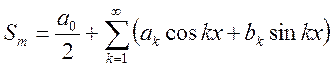 ,
, ![]() - это
надо доказать!
- это
надо доказать!
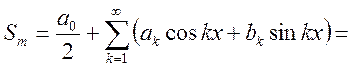 (представим
коэффициенты Фурье)
(представим
коэффициенты Фурье)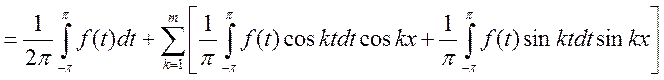
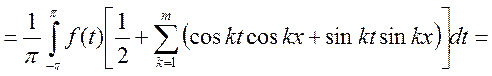
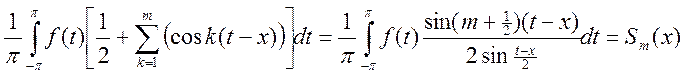

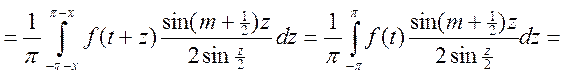
(т.к. функция периодич. по z![]() можем х положить (в пределах) = 0, при этом интегралы
не изменяются)
можем х положить (в пределах) = 0, при этом интегралы
не изменяются)
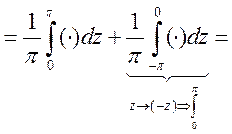
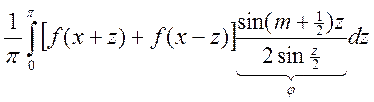 . Рассмотрим разность
. Рассмотрим разность 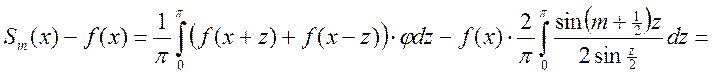
 . Если бы
. Если бы  была непрерывна то по лемме Римана интеграл
была непрерывна то по лемме Римана интеграл
![]() . По пр. Лапиталя
. По пр. Лапиталя ![]() по
z
по
z ![]() , устремляем
, устремляем ![]() ( по
теореме Римана)
( по
теореме Римана)
Теорема: всякая непрерывная функция![]() ,
заданная на компакте
,
заданная на компакте ![]() , равномерно непрерывна.
, равномерно непрерывна.
Доказательство: надо доказать,
что равномерна, непрерывна. Докажем от противного ![]() . Пусть
. Пусть
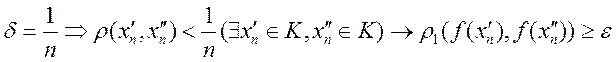 . Выделяем
. Выделяем ![]() и из
второй
и из
второй ![]() (причем номера
(причем номера ![]() совпадает
с номером первой послед.). Докажем, что
совпадает
с номером первой послед.). Докажем, что ![]() :
рассм.
:
рассм. ![]() (по нер-ву
(по нер-ву ![]() )
)  .
. 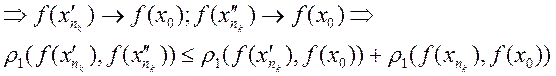
Но если подставить ![]() противоречие.
противоречие.
Теорема о единственности для гармонической функции
Теорема:
Если ![]()
![]() ,
, ![]() ,
Функция
,
Функция ![]() класса
класса ![]() . Тогда
. Тогда
![]() в D, т.е
в D, т.е ![]() .
.
Доказательство:
1) 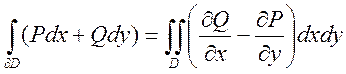 -
формула Грина.
-
формула Грина.
2) Положим 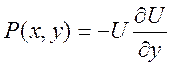 , а
, а 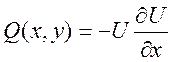 , где
, где ![]() любая функция класса
любая функция класса ![]() . Тогда 1 имеет вид:
. Тогда 1 имеет вид:

3) В качестве U во
2 берём гармоническую функцию 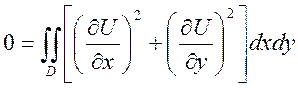
4) Т.к. интеграл = 0 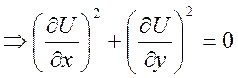
5) 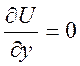 ,
,
 ,
, ![]()
6) т.к. существуют частные
производные ![]()
7) т.к. ![]() , то
, то ![]()
Для трех переменных:
Теорема:
Если ![]()
![]() ,
, ![]() ,
Функция
,
Функция ![]() класса
класса ![]() . Тогда
. Тогда
![]() в B , т.е
в B , т.е ![]() .
.
Доказательство:
1) Ф-ла Гаусса –
Остроградского: 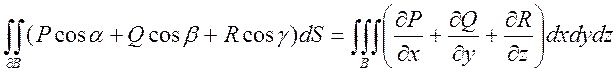
2) 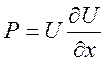 ,
,
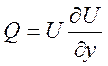 ,
, 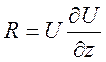 ,
положим тогда формула
,
положим тогда формула 
3) В качестве ![]() и
и ![]()
![]() слева
слева 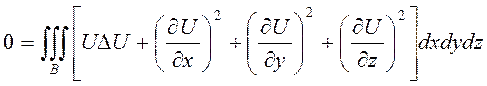
4) 
5)  ,
,
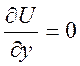 ,
, 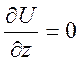 ,
, ![]()
6) ![]()
7) т.к ![]() , то C=0 в B
, то C=0 в B
Теорема: всякое сжимающее отображение полного метрического пространства М в себя имеет неподвижную точку, и притом только одну.
Доказательство: (методом послед. приближений) ![]() (
(![]() - произвольная точка) и
строится
- произвольная точка) и
строится ![]()
![]() .
Докажем
.
Докажем ![]() - неподвижная точка:
- неподвижная точка: ![]() (т.к. сжат.)
(т.к. сжат.)![]() т.е.
т.е. ![]() , где k- любой. Рассм.
, где k- любой. Рассм.
![]() (т.е. добавили точку
(т.е. добавили точку ![]() и воспользовались неравенством
и воспользовались неравенством ![]() )
)![]()
![]() (воспольз.
оценкой)
(воспольз.
оценкой) 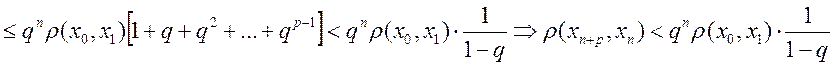 (получим оценку)
(получим оценку) 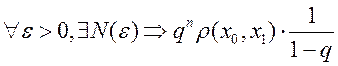 ,
что
,
что 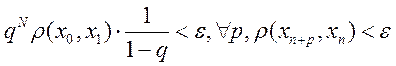 - последовательность фундаментальна, а т.к.
пр-во полное
- последовательность фундаментальна, а т.к.
пр-во полное ![]() . Теперь док-ем, что x-неподвижная
точка. Рассм. расст.
. Теперь док-ем, что x-неподвижная
точка. Рассм. расст. ![]() при
при ![]() ,
, ![]() , точка неподвижна. Докажем, что она
единственна:
, точка неподвижна. Докажем, что она
единственна: ![]()
![]() и
и ![]()
![]() противоречие. Теорема
доказана.
противоречие. Теорема
доказана.
Теорема о неявной функции.
![]() ,
, ![]() ,
, ![]() . Пусть
выполнено условие:
. Пусть
выполнено условие:
1) вектор – функция ![]() непрерывно диф-ма в
непрерывно диф-ма в ![]() ,
т.е.
,
т.е. ![]() , т.е. каждая компонента обладает этими
свойствами ( имеет непрерывные частные производные в
, т.е. каждая компонента обладает этими
свойствами ( имеет непрерывные частные производные в ![]() )
)
2) существует точка ![]() , такая что
, такая что ![]()
3) Определитель м-цы 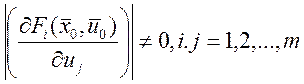 . Тогда существует окрестность точки
. Тогда существует окрестность точки ![]() , такая что в этой окрестности определена
единственная непрерывно – диф-мая неявная вектор-функция
, такая что в этой окрестности определена
единственная непрерывно – диф-мая неявная вектор-функция ![]() , т.е
, т.е ![]()
Доказательство:
Рассмотрим три случая:
1) а) ![]() , а
, а ![]() - тоже.
- тоже.
Тогда ![]() ,
а
,
а ![]() - интервалы. И
- интервалы. И ![]() -
функция (веществ.) двух переменных
-
функция (веществ.) двух переменных ![]() и
и ![]() , заданная в прямоугольнике. Тогда
существует точка
, заданная в прямоугольнике. Тогда
существует точка ![]() ,
, ![]() и
и ![]() непрерывны в
непрерывны в ![]()
![]() , а
, а 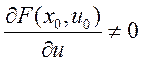 - это условие теоремы. Тогда по теореме
существует окрестность точки
- это условие теоремы. Тогда по теореме
существует окрестность точки ![]() , в которой
, в которой ![]() - непрерывно диф-ма и
- непрерывно диф-ма и ![]() - это надо доказать.
- это надо доказать.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.