Оптимізація просторово-часових параметрів функціонування системи керування, що навчається, страница 8

                    J₁

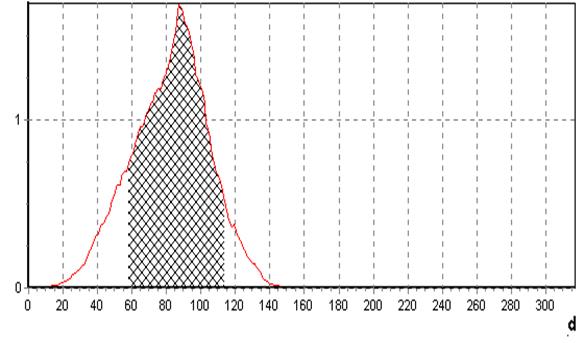
Рис. 4.6. Залежність КФЕ від радіуса контейнера 

На рис. 4.6 робоча область визначення КФЕ зліва обмежується областю, де перша достовірність дорівнює   і справа - областю, де помилка другого роду приймає значення   Оптимальне значення    радіуса контейнера    визначається для    і, як видно з рис. 4.5, воно дорівнює 87 одиницям кодової відстані. Для контейнера класу    оптимальне значення його радіуса дорівнює    при міжцентровій відстані 166, тобто має місце перетин класів    і  .

Порівняльний аналіз ефективності навчання за базовим алгоритмом навчання (рис. 4.3) і за паралельним алгоритмом оптимізації контрольних допусків на ознаки розпізнавання (рис. 4.5) показує збільшення в останньому випадку значення КФЕ навчання (3.5.5) (  проти    за базовим алгоритмом). Причина низької ефективності  навчання за базовим алгоритмом саме і полягала в тому, що СКД на ознаки розпізнавання не була оптимальною. З іншого боку, наведений приклад оптимізації контрольних допусків за паралельним алгоритмом свідчить у відповідності з теоремою 4.4.2, що він не забезпечує побудову безпомилкового вирішального правила і потребує оптимізації інших параметрів навчання, що входять у структуру (2.3.7). 

4.5 Оптимізація контрольних допусків за зведеним полем

Один із шляхів застосування МФСВ для вирішення проблеми визначення оптимальної в інформаційному розумінні СКД на ознаки розпізнавання передбачає побудову зведеного поля допусків. Такий підхід дозволяє звести багатофакторну задачу планування експерименту до вибору на зведеному полі значень оптимальних контрольних допусків за інформаційним КФЕ і оберненого відображення цих значень на поля допусків відповідних ознак.

Розглянемо математичні задачі, пов’язані з побудовою зведеного поля допусків. Будемо вважати шкалою відрізок числової прямої  , кінці якого є натуральними числами:  N. Для будь-яких двох шкал    існує тільки одне зростаюче лінійне відображення , таке, що  . Це відображення будемо називати прямим перетворенням шкал [248]:

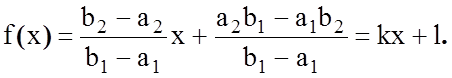                                                    (4.5.1)

Обернене перетворення шкал, як відомо, має вигляд:

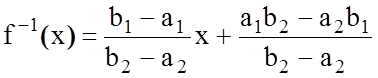                                  .                                    (4.5.2)

Позначимо через  М  множину всіх чисел, які записуються у вигляді   кінцевого десятичного дробу. Вона є підмножиною множини  Q  всіх раціональних чисел. Точний опис множини  М  дає така лема  [249, c.280].

Л е м а 4.5.1. Для того, щоб раціональне число подавалося у  вигляді кінцевого дробу, необхідно та достатньо, щоб його знаменник (у нескорочуваному запису) мав вигляд  N=N {0}).

Кількість значущих цифр після коми у такого числа не перебільшує . Таким чином,

                               М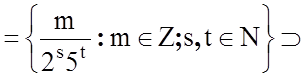Z,

де  Z – множина  всіх цілих чисел. Відносно операцій складання та  множення  М  утворює кільце, тобто сума, різниця та добуток чисел з  М  так само належать М.

Л е м а 4.5.2. Нехай  . Тоді, якщо 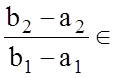 М,  то і  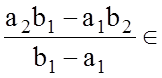М.

Повертаючись до перетворення  (4.5.1) відзначимо, що оскільки його коефіцієнти раціональні, то  f  переводить множину  Q  в себе. При цьому виникає питання, які перетворення  шкал    переводять числа з кінцевим десятичним записом у числа того ж вигляду, тобто, коли з включення  М витікає  М. Такі перетворення будемо називати допустимими. Зрозуміло, що композиція допустимих перетворень є так само допустимим перетворенням. Тотожнє відображення будь-якої шкали на себе є допустимим. Разом з тим,  перетворення, яке обернене до допустимого, не обов’язково є допустимим. У цьому легко переконатися на прикладі:   допустимо, а обернене перетворення не є допустимим.

Т в е р д ж е н н я  4.5.1. Для того, щоб перетворення шкал (4.5.1) було допустимим, необхідно та достатньо, щоб його коефіцієнти  k,l  належали  М.

Достатність умови твердження витікає з того, що  М  утворює кільце. Для доведення необхідності припустимо, що  – допустиме перетворення. Тоді М, звідки  М. Але тоді  М  і значить  М.

Твердження 4.5.1 можна підсилити.