Поля. Алгебраические операции для элементов поля. Комплексное число. Алгебраическая форма записи комплексного числа, страница 9

Отличный от нуля минор порядка r называется базисным минором A.

Строки (столбцы), на которых построен базисный минор, называются базисными.

Теорема№1: Любой столбец (строка) матрицы A является линейной комбинацией ее базисных столбцов (базисных строк).

Д-во: поскольку при произвольн. переменах столбцов(строк) определитель сохр. св-ва =0, то можно, не нарушая общности, считать, что базисы располож. на первых r строках и первых r столбцах матрицы A (где r – ранг матрицы A)рассмотрим определитель порядка r+1: D=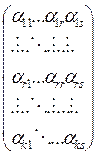(где s – люб. число 1,…,m, а k 1,…,n) если k≤r, то для люб. s=>D=0, т.к. 2-е строки определителя одинак.; если s≤r, то для люб. k D=0, т.к. 2 столбца определителя одинак.; если k>r и s>r, то D=0, т.к. порядка r+1, для люб. k, s D=0. Разложим опр-ль D по последн. строке a_k1A_k1+…+a_kpA_kp+a_ksA_ks=0. Эти алгебраич. дополн. не завис. от номера k. Поэтому вместо A_k1,…,A_kp, с₁,…,с_s(ХЗ)

Теорема№2: Если один из столбцов определителя D является линейной комбинацией других его столбцов, то D=0

Теорема№3: Если D=0, то у него имеется столбец, являющийся линейной комбинацией других столбцов

Теорема№4: Определитель D=0 тогда и только тогда, когда его строки линейно зависимы.

Теорема№5: Ранг системы векторов-столбцов матрицы A равен рангу матрицы. Векторы, отвечающие базисным столбцам образуют базу системы векторов-столбцов A

Теорема№6: Размерность линейной оболочки системы векторов-столбцов матрицы A равна рангу матрицы A. Векторы, отвечающие базисным столбцам A, образуют базис линейной оболочки.

Теорема№7: Если ранг матрицы A меньше, чем число ее столбцов, то столбцы A линейно зависимы. Если ранг матрицы A равен числу столбцов, то столбцы A – линейно независимы.

Теорема№8: Всякие (r+1) столбцов матрицы A ранга r линейно зависимы.

Теорема№9: Ранг любой матрицы равен максимальному числу линейно независимых столбцов

Теорема№10: Максимальное число линейно независимых строк любой матрицы совпадает с максимальным числом линейно независимых столбцов

Системы линейных алгебраических уравнений (СЛАУ)

Ax = 0

a₁x₁+a₂x₂+…+a_mx_m = q

a_i – столбцы A

Однородная СЛАУ всегда совместна, т.к. она всегда обладает тривиальным или нулевым решением.

Теорема№1:

а) Однородная СЛАУ нетривиально совместна тогда и только тогда, когда ранг матрицы A меньше числа неизвестных

б) Если ранг матрицы равен числу неизвестных, то однородная СЛАУ не имеет ненулевых решений

в) Если ранг матрицы A меньше числа неизвестных, то ненулевые решения существуют

Совокупность линейно независимых решений однородной СЛАУ называется фундаментальной системой решений, если всегда решение этой системы может быть представлено в виде линейной комбинации векторов этой совокупности.

Теорема№2: Общее решение неоднородной СЛАУ есть сумма какого-либо частного решения cоответствующей неоднородной СЛАУ и общего решения соответствующей однородной СЛАУ.

Теорема Кронекера-Капелли

A – основная матрица

A₁ (A|b) – расширенная матрица

Теорема: Неоднородная СЛАУ совместна тогда и только тогда, когда ранги матриц A и A₁ совпадают.

Доказательство:

Необходимость: Пусть система совместна, тогда правая часть b – есть линейная комбинация столбцов матрицы A (rgA = rgA₁)

Достаточность: Если rgA=rgA₁, то r базисных столбцов A будут базисными и для A_1. Правая часть b представляет собой некоторую линейную комбинацию базисных столбцов и представляет собой линейную комбинацию всех столбцов основной матрицы, т.е система совместна.

Теорема: мн-во всех решений однородной СЛАУ с n неизвестными образует подпр-во размерности n-k, где k – ранг матрицы системы.